Executive Summary
This project is a “digital restoration” of Aneesur Rahman’s seminal 1964 paper, Correlations in the Motion of Atoms in Liquid Argon. While the physics of liquid argon is a solved problem, the challenge lies in bridging the gap between 1960s mainframe constraints and 2025 software architecture.
I replicated the simulation using LAMMPS and built a custom, production-grade Python analysis pipeline to process the trajectory data. The project demonstrates how modern tooling (uv, type hinting, vectorized NumPy) can transform academic “write-once” scripts into a robust, reproducible research toolkit.
Engineering Architecture
The Analysis Pipeline
Instead of writing ad-hoc scripts, I architected a modular Python package (argon_sim) designed for performance and maintainability.
- Intelligent Caching System: MD analysis is compute-intensive ($O(N^2)$). I implemented a decorator-based caching layer (
@cached_computation) that hashes source file modification times and function arguments. This ensures expensive calculations (like RDF or Van Hove correlations) are only re-run when the underlying trajectory or parameters actually change. - Vectorization & Optimization: To handle the $N^2$ complexity of pair-wise interactions without C++ extensions, I utilized NumPy broadcasting. For example, the Mean Square Displacement (MSD) calculation is fully vectorized, with a fallback “chunked” implementation to handle memory overflows on smaller machines.
- Modern Python Tooling:
- Dependency Management: Used
uvfor deterministic environment locking (sub-second resolution). - Type Safety: 100% type-hinted codebase for static analysis compliance.
- Automation: A robust
Makefileabstracts the complex workflow (simulation → analysis → figure generation) into single commands (e.g.,make figure-5).
- Dependency Management: Used
The Simulation Strategy
I used LAMMPS for the MD engine but strictly adhered to Rahman’s physical parameters while modernizing the stability mechanisms.
- Integration: Replaced Rahman’s predictor-corrector method with the modern standard Velocity Verlet algorithm (2 fs timestep).
- Equilibration: Unlike the 1964 paper, which used simple velocity scaling, I implemented a 500 ps NVT equilibration phase to properly melt the FCC crystal structure before the NVE production run.
- Intellectual Honesty: The
in.argonscript explicitly documents every deviation from the original methodology (e.g., energy minimization) and the justification for ensuring numerical stability.
Key Results & Validation
The replication achieved high quantitative agreement with the historical data, validating both the simulation parameters and the custom analysis code.
| Property | Rahman (1964) | This Work | Notes |
|---|---|---|---|
| Diffusion Coefficient ($D$) | $2.43 \times 10^{-5}$ cm²/s | $2.47 \times 10^{-5}$ cm²/s | Agreement within 2% |
| RDF First Peak | $3.7$ Å | $3.82$ Å | Slight shift |
| Velocity Dist. Width ($e^{-1/2}$) | $1.77$ | $1.77$ | Exact match to theoretical Maxwell-Boltzmann |
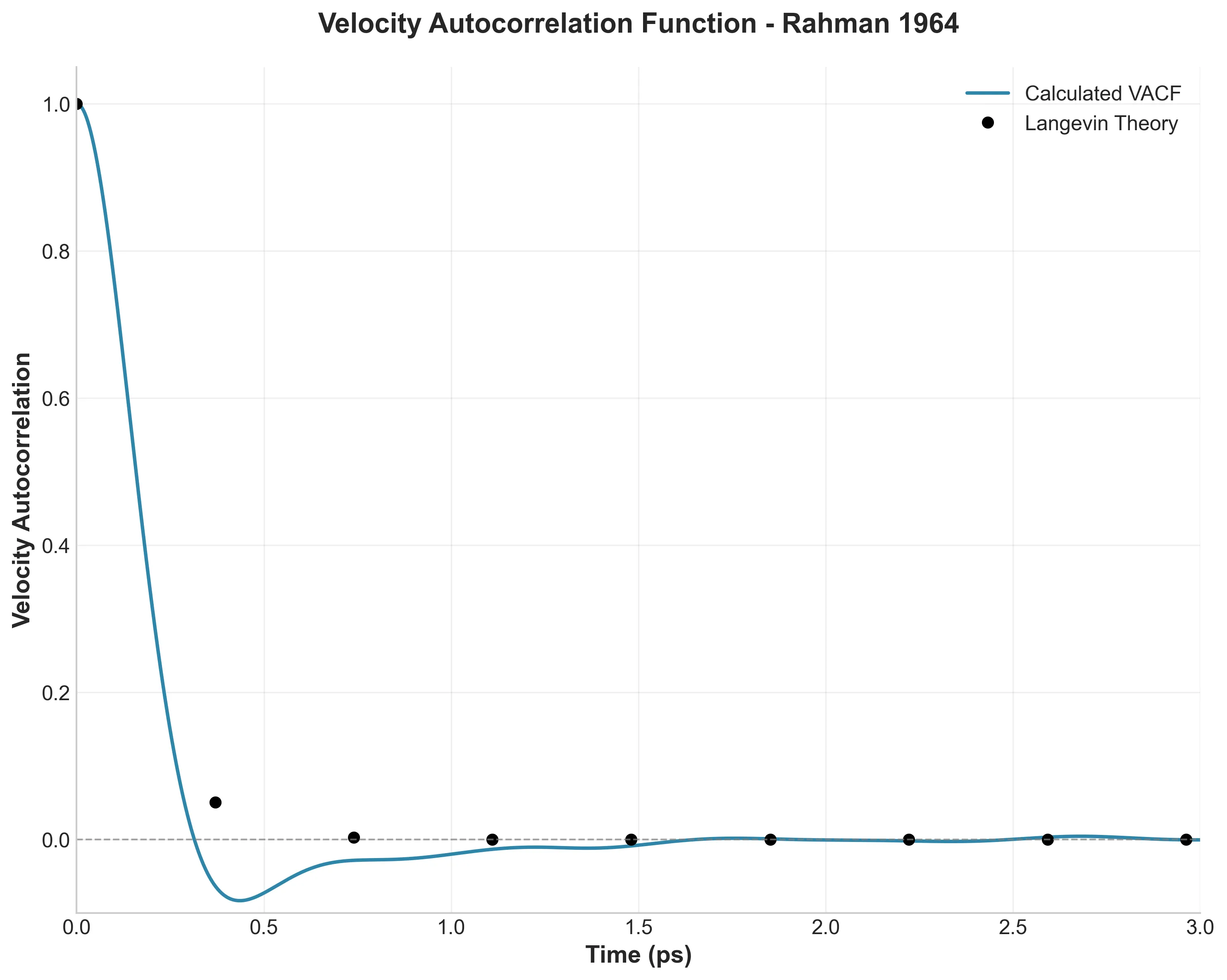
Visual Replication
I used Matplotlib to digitally recreate Rahman’s hand-drawn plots, confirming signatures like the negative region in the Velocity Autocorrelation Function (VACF), which provided the first evidence of the “cage effect” in simple liquids.
Challenges & Learnings
- Unit Hell: Rahman’s paper uses a mix of reduced units and CGS. Mapping these to LAMMPS’s
realunits required a dedicatedconstants.pymodule and rigorous unit testing to prevent dimensional errors. - Fourier Transforms: Calculating the Structure Factor $S(k)$ from $g(r)$ required implementing a manual 3D Fourier transform for spherical symmetry, as standard FFT packages do not account for the radial shell integration implicit in liquid structure analysis.
- Code as a Liability: Early in the project, I realized that re-running analysis scripts was becoming a bottleneck. This drove the decision to build the caching infrastructure, reinforcing the lesson that investing in developer tooling pays off even in small-scale scientific projects.
Related Work
The full methodology and physics are documented in the companion blog post:
