Overview

This project implements the classic 2D Müller-Brown potential in PyTorch as a ground-truth testbed for machine-learning-in-molecular-dynamics (ML-MD) work. The potential is a torch.nn.Module that computes forces two ways: a hand-derived analytical gradient (the default, compiled with torch.compile) and torch.autograd.grad (a reference the analytical path is checked against). On an Apple M1 Max, the analytical kernel runs about 4x faster than autograd (3-7x depending on batch size; 100 warm-up iterations, then the median of 5 runs of 1000), because it skips autograd’s graph construction inside the force loop.

The energy is deliberately left uncompiled so that second derivatives (the Hessian via autograd) keep working, since torch.compile does not support double-backward; the force, the hot path, is the compiled function.

Features

  • Dual force kernels: a hand-derived analytical gradient (compiled) for fast simulation, and an autograd mode for differentiation and as the correctness reference the analytical path is tested against.
  • BAOAB Langevin integrator: the BAOAB splitting scheme (Leimkuhler & Matthews, 2013), which solves the friction-plus-noise step exactly and samples the canonical distribution accurately (exactly so for a harmonic oscillator).
  • Device-agnostic: potential, forces, and simulation are plain PyTorch tensor operations that run on CPU or CUDA; the included benchmark measures CPU.
  • Modular architecture: physics (MuellerBrownPotential), numerics (LangevinSimulator), visualization, and HDF5 I/O are separated, with a CLI orchestrating demo, single-run, batch, and plot-regeneration modes.

Usage

The package installs editable with uv sync and imports as a normal package:

from muller_brown import MuellerBrownPotential, LangevinSimulator

It provides a fast, differentiable Müller-Brown potential and a Langevin sampler for testing ML-MD algorithms against a known-exact surface.

Results

Architecture

  • Physics module: the energy surface is a torch.nn.Module with the potential parameters held as registered buffers, so device and dtype move with the module.
  • Analytical force kernel: the analytical Jacobian is implemented directly and compiled with torch.compile(dynamic=True), bypassing autograd-graph construction during long simulations.
  • Vectorized execution: kernel operations are vectorized over particles, so an ensemble runs in roughly the same wall time as a single particle (the per-step cost is dominated by the fixed force call and noise draw).
  • Device-agnostic: all operations move to CUDA via native tensor handling; the benchmark and tests run on CPU.

Performance

A force-throughput benchmark (analytical vs autograd) across batch sizes from 2 to roughly 50,000 particles, on an Apple M1 Max:

  • The analytical kernel is about 4x faster than autograd (3-7x across batch sizes).
  • Per-particle force time drops below 1 microsecond at large batch sizes.
  • Throughput rises with batch size and saturates for large ensembles.

Validation

The sampler is checked against statistical mechanics, not just run:

  • Deterministic tests: the documented minima and saddles have the correct Hessian signatures; the analytical force matches torch.autograd.grad; energy is conserved in the frictionless (NVE) limit; float32 matches float64; and HDF5 round-trips preserve the data.
  • Statistical tests: the sampler reproduces equipartition, the harmonic-oscillator distributions, and the Müller-Brown Boltzmann mean energy against a grid-integrated reference; a separate convergence study confirms the integrator’s kinetic-temperature bias vanishes as the timestep squared.

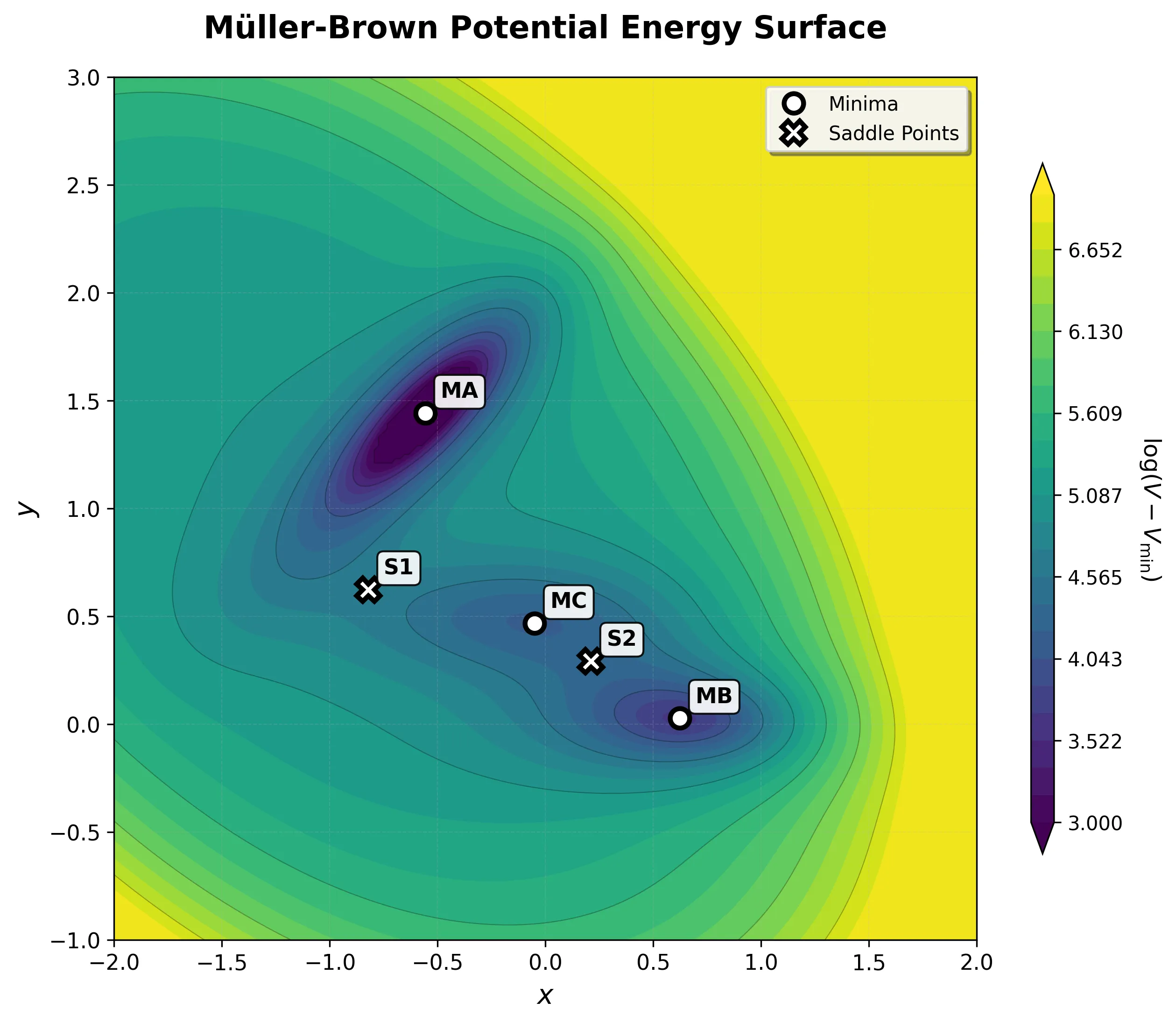
Molecular Dynamics

Langevin simulations on the surface show particle motion within energy basins, thermal fluctuations around the minima, and barrier-crossing transitions between wells, visualized as trajectories on the potential surface.

Simulation Videos

These videos demonstrate Langevin dynamics simulations on the Müller-Brown potential surface:

A Basin Dynamics: Particle motion and thermal fluctuations around the A minimum.

B Basin Dynamics: Exploration of the deeper B minimum energy well.

Transition Path: Particle transitioning between energy basins, demonstrating barrier crossing.

This implementation is documented in detail in: