Written during my sophomore year, this project was an attempt to look inside the “black box” of the world’s fastest Fourier transform library: FFTW.
Overview
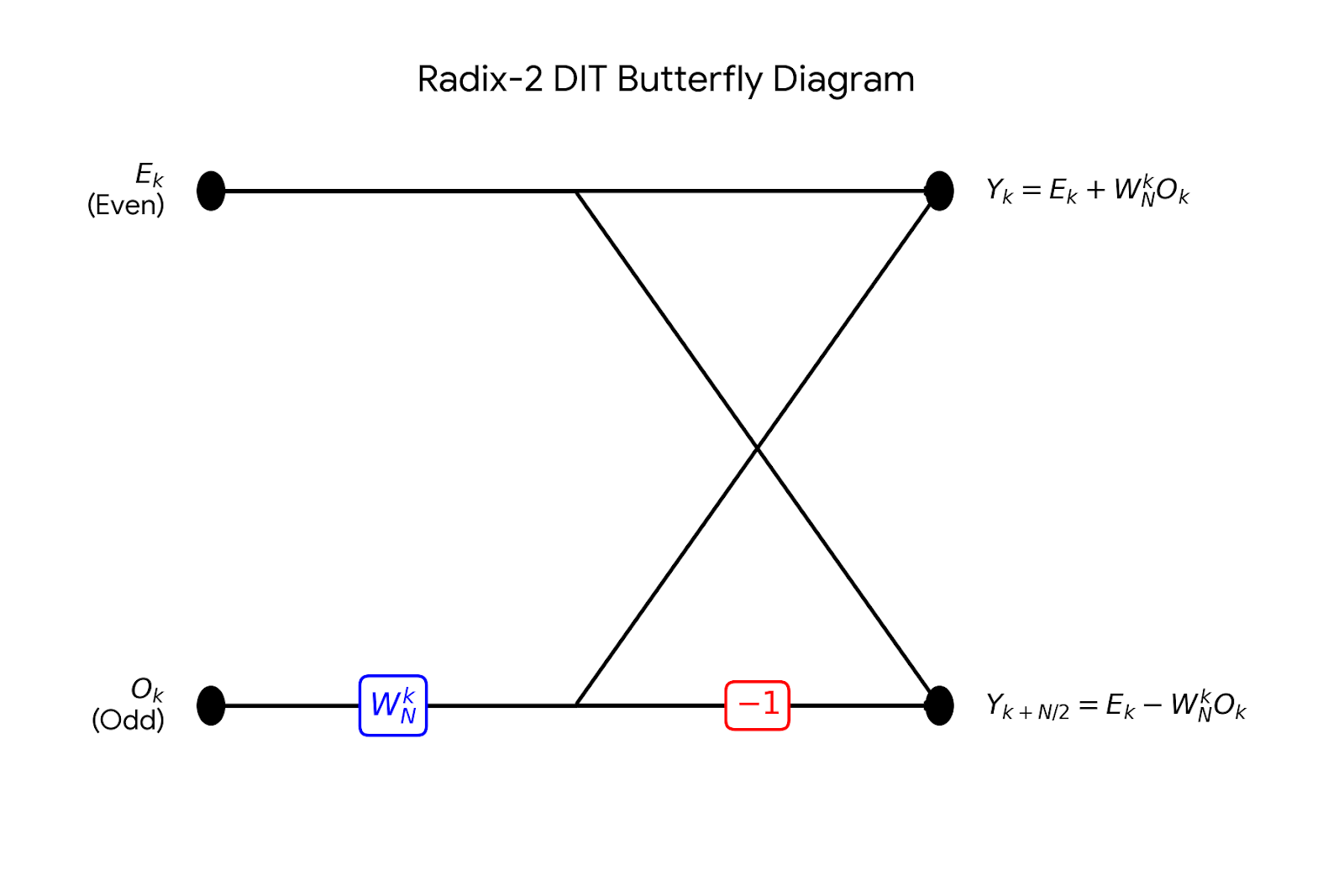
I sought to replicate the logic of FFTW’s genfft: a metaprogram that generates straight-line, highly optimized C code. The goal was to understand how abstract algebra (group theory) could be translated into efficient machine code through symbolic manipulation.
Features
This was my first deep dive into functional metaprogramming and compiler theory:
- Symbolic AST: Modeled mathematical operations as a Directed Acyclic Graph (DAG) in Haskell (
data Node), separating the definition of the math from its execution. - Algebraic Simplification: Implemented a symbolic optimization pass that pruned operations at compile-time (e.g., eliminating multiplications by $1$, $0$, or $-1$) before code generation.
- Monadic State Management: Used Haskell’s
StateMonad to manage the graph construction and memoization, ensuring common subexpressions (like reusable cosine factors) were calculated only once. - Code Generation: The system outputted unrolled, straight-line C code (e.g.,
fftw4.c), mimicking the “codelets” used by the actual FFTW library.
Usage/Gameplay
The compiler is run via the command line, taking the desired FFT size as input and outputting the optimized C code.
Results
Looking back, this project represents a pivotal moment where I moved from “writing programs” to “writing tools that write programs.”
- The “Magic”: It demystified high-performance computing. I learned that speed often comes from unrolling recursion and managing register pressure at compile time alongside writing fast loops.
- The “Rough Edges”: The scheduler (coloring nodes Red/Blue for register allocation) was a heuristic approximation of the optimal Aho-Johnson-Ullman algorithm.
- Legacy: The core lesson that domain-specific compilers can outperform hand-tuned generic code remains relevant to my current work in optimizing scientific computing kernels.