Understanding Generative Models
Before diving into Generative Adversarial Networks (GANs), let’s establish what we’re trying to accomplish with generative models.
The core goal: Create a system that can generate new, realistic data that’s never been seen before, yet appears to come from the same distribution as our training data.
Imagine having a model that can create images, text, or audio that are difficult to distinguish from human-created content. This is the goal of generative modeling.
The Mathematical Foundation
Generative models aim to estimate the probability distribution of real data. If we have parameters $\theta$, we want to find the optimal $\theta^*$ that maximizes the likelihood of observing our real samples:
$$ \theta^* = \arg\max_\theta \prod_{i=1}^{n} p_\theta(x_i) $$
This is equivalent to minimizing the distance between our estimated distribution and the true data distribution. A common distance measure is the Kullback-Leibler Divergence, where maximizing log-likelihood equals minimizing KL divergence.
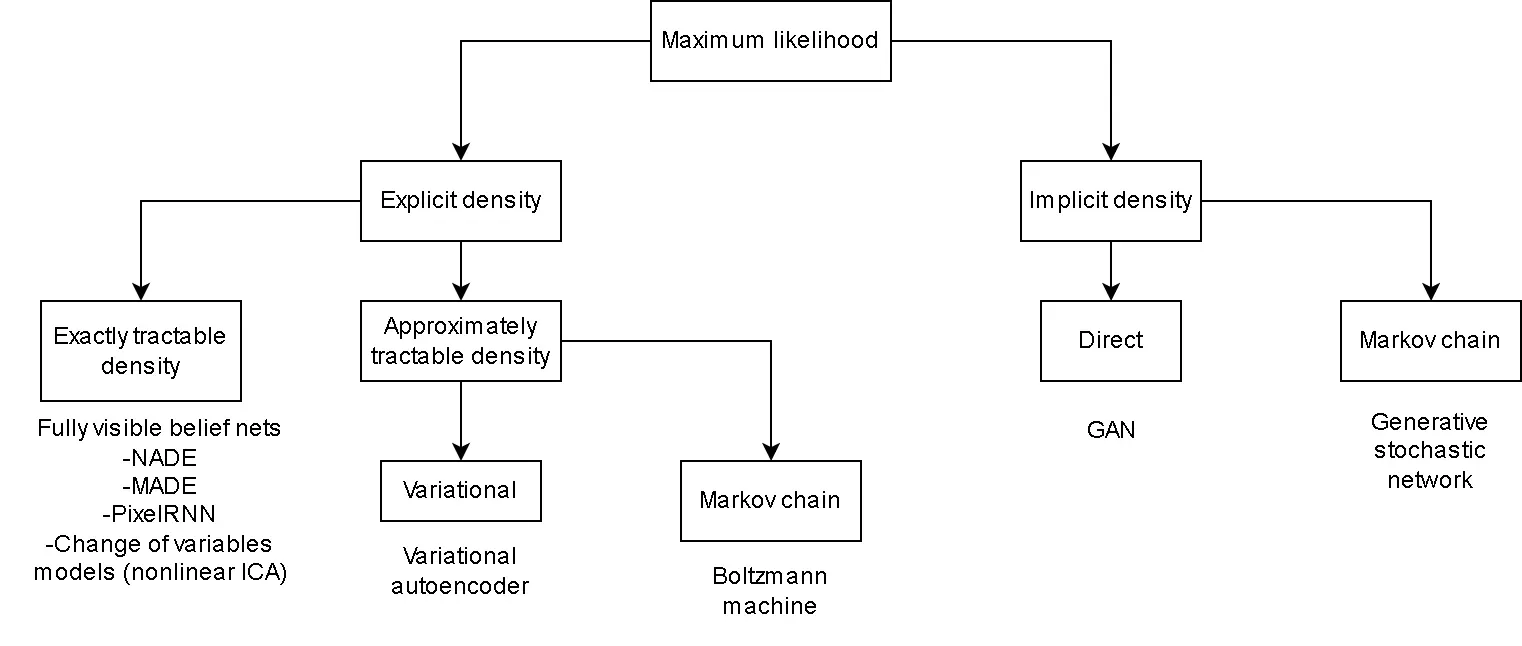
Two Approaches to Generative Modeling
Explicit Distribution Models
These models define an explicit probability distribution and refine it through training.
Example: Variational Auto-Encoders (VAEs) require:
- An explicitly assumed prior distribution
- A likelihood distribution
- A “variational approximation” to evaluate performance
Implicit Distribution Models
These models learn to generate data without explicitly defining a probability distribution. Instead, they sample from their learned distribution indirectly.
This is where GANs shine – they’re implicit generative models that learn through adversarial competition.
Taxonomy of Deep Generative Models: GANs fall into the implicit density category, learning distributions through adversarial training rather than explicit modeling. Source: NeurIPS 2016 tutorial on Generative Adversarial Networks
The GAN Architecture: A Game of Deception
Generative Adversarial Networks get their name from three key components:
- Generative: They create new data
- Adversarial: Two networks compete against each other
- Networks: Built using neural networks
The genius lies in the adversarial setup: two neural networks locked in competition, each pushing the other to improve.
GAN Data Flow: The generator creates fake samples from random noise, while the discriminator tries to distinguish real from fake data. This adversarial competition drives both networks to improve.
The Generator: The Forger
Role: Create convincing fake data from random noise
The generator network $G$ learns a mapping function: $$z \rightarrow G(z) \approx x_{\text{real}}$$
Where:
- $z$ is a random latent vector (the “noise”)
- $G(z)$ is the generated sample
- The goal is making $G(z)$ indistinguishable from real data
Key insight: The latent space $z$ is continuous, meaning small changes in $z$ produce smooth, meaningful changes in the generated output.
The Discriminator: The Detective
Role: Distinguish between real and generated samples
The discriminator network $D$ outputs a probability: $$D(x) = P(\text{x is real})$$
- $D(x) \approx 1$ for real samples
- $D(x) \approx 0$ for fake samples
Think of it as an “authenticity detector” that gets better over time.
The Adversarial Competition
This is where the magic happens. The generator and discriminator have directly opposing objectives:
| Generator Goal | Discriminator Goal |
|---|---|
| Fool the discriminator | Correctly classify all samples |
| Minimize $D(G(z))$ | Maximize $D(x_{\text{real}})$ and minimize $D(G(z))$ |
| “Create convincing fakes” | “Never be fooled” |
This creates a dynamic where both networks continuously improve:
- Generator creates better fakes to fool the discriminator
- Discriminator becomes better at detecting fakes
- The cycle continues until equilibrium
The Adversarial Training Process: Through competition, both networks improve. The generator learns to create increasingly realistic samples while the discriminator becomes more discerning.
Learning Through Metaphors
Sometimes the best way to understand complex concepts is through relatable analogies. Here are three metaphors that capture different aspects of how GANs work.
🎨 The Art Forger vs. Critic
Generator = Art Forger
Discriminator = Art Critic
A criminal forger tries to create fake masterpieces, while an art critic must identify authentic works. Each interaction teaches both parties:
- The forger learns what makes art look authentic
- The critic develops a keener eye for detecting fakes
- Eventually, the forger becomes so skilled that even experts can’t tell the difference
This captures the adversarial nature and continuous improvement aspect of GANs.
💰 The Counterfeiter vs. Bank Teller
Generator = Counterfeiter
Discriminator = Bank Teller
Day 1: Criminal brings a crayon drawing of a dollar bill. Even a new teller spots this fake.
Day 100: The counterfeiter has learned better techniques. The teller has developed expertise in security features.
Day 1000: The fake money is so convincing that detecting it requires advanced equipment.
This illustrates the progressive improvement and escalating sophistication in both networks.
🦜 The Parrot vs. Sibling
Generator = Pet Parrot
Discriminator = Younger Brother
You sit behind curtains with your parrot. The parrot tries to mimic your voice to fool your brother about which curtain you’re behind. Successful mimicry gets treats.
Initially, the parrot’s attempts are obvious. But through practice, the parrot develops the ability to closely mirror your voice.
This shows how GANs can learn to replicate complex patterns through reward-based competition.
The Mathematical Foundation
Now let’s examine the mathematical framework that makes GANs work. The core of GAN training is solving a minimax optimization problem.
The Minimax Objective
$$ \min_{G} \max_{D} V(D, G) = \mathbb{E}{x \sim p{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] $$
Breaking this down:
| Component | Meaning | Goal |
|---|---|---|
| $\mathbb{E}{x \sim p{\text{data}}(x)}[\log D(x)]$ | Expected log-probability for real data | Discriminator wants to maximize this |
| $\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$ | Expected log-probability for fake data being labeled fake | Discriminator wants to maximize this |
| Generator wants to minimize this |
Why “Minimax”?
- Discriminator ($D$): Tries to maximize the objective → Better at distinguishing real from fake
- Generator ($G$): Tries to minimize the objective → Better at fooling the discriminator
The Training Process
The beauty of GANs lies in their alternating optimization:
- Fix $G$, train $D$: Make the discriminator optimal for the current generator
- Fix $D$, train $G$: Improve the generator against the current discriminator
- Repeat: Continue until reaching Nash equilibrium
Theoretical Goal: Nash Equilibrium
At convergence, the discriminator outputs $D(x) = 0.5$ for all samples, meaning it can’t distinguish between real and fake data. This indicates that $p_{\text{generator}} = p_{\text{data}}$ – our generator has learned the true data distribution.
What’s Next?
Now that you understand the fundamentals of GANs, you’re ready to explore the rich ecosystem of GAN variants and improvements. Each addresses specific challenges like training stability, mode collapse, or convergence issues.
Continue your GAN journey: Check out my follow-up post on GAN Objective Functions, where we explore various GAN architectures including WGAN, LSGAN, and many others that have shaped the field. For the complete learning path, see the Understanding GANs series.
Acknowledgments: This post was inspired by the excellent survey “How Generative Adversarial Networks and Their Variants Work: An Overview of GAN” – an invaluable resource for understanding the GAN landscape.