Some papers change everything. Aneesur Rahman’s 1964 work, “Correlations in the Motion of Atoms in Liquid Argon”, is one of them. Just eight pages in Physical Review, but it basically invented molecular dynamics simulation.
Rahman’s idea was simple but radical: use a computer to solve Newton’s equations for 864 argon atoms and watch what happens. This was 1964—computers were room-sized behemoths, and the idea of simulating atoms was almost science fiction. But it worked.
For the first time, someone could “see” how atoms move in a liquid. The results weren’t just pretty pictures—they revealed fundamental physics. Rahman discovered that atoms in liquids don’t just diffuse randomly; they get trapped by their neighbors and bounce back, creating the “cage effect” that’s central to how we understand liquids today.
I wanted to see if I could recreate Rahman’s results using modern tools. This project, available on GitHub, uses Python for analysis and LAMMPS for the simulation. The goal was simple: run the exact same conditions as 1964 and see what we get.
The Setup: Modern Tools, Classic Physics
I stayed true to Rahman’s original conditions while using better software. The core parameters in my LAMMPS input script match exactly:
- System: 864 Argon atoms.
- Interaction: Lennard-Jones potential with parameters $\sigma = 3.4$ Å and $\epsilon/k_B = 120$ K.
- Thermodynamic State: A target temperature of $94.4^\circ$K and a density of $1.374 \text{ g cm}^{-3}$.
But I used some modern best practices that weren’t available in 1964:
- Energy minimization before starting dynamics to remove bad contacts from the crystal lattice
- Proper equilibration with 500 ps in the NVT ensemble to let the crystal melt into a real liquid
- Better integration using Velocity Verlet with a 2 fs timestep instead of Rahman’s custom 10 fs method
The production run was 10 ps in the NVE ensemble, generating 5001 frames. Temperature stayed within 1% of target with an RMS fluctuation of just 0.0165—much more stable than what Rahman could achieve.
The Results: 60 Years Later
My Python analysis toolkit processes the LAMMPS trajectory to recreate each figure from the original paper. The agreement is remarkable.
System Check: Temperature and Velocities
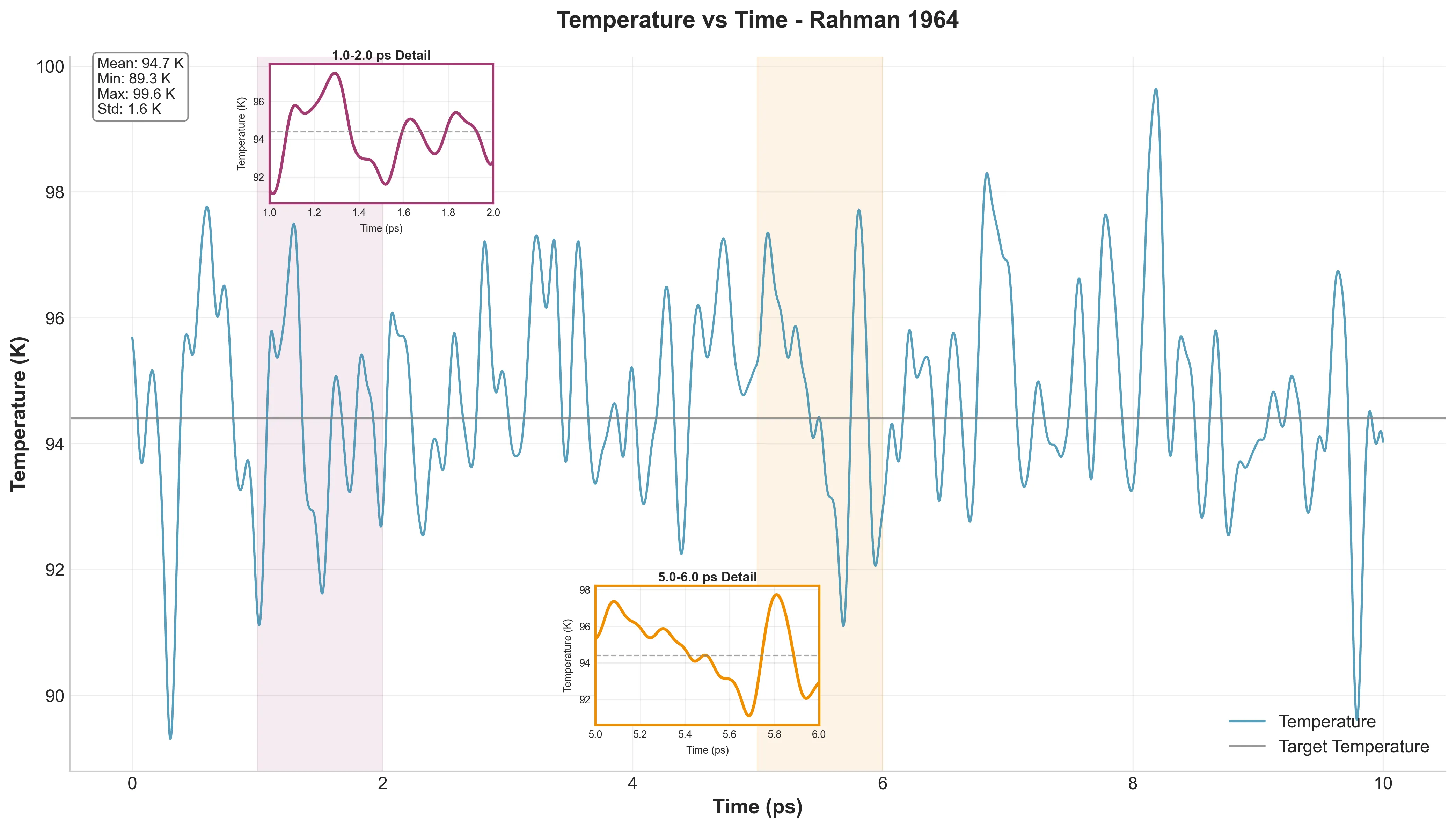
Temperature vs. Time - 5001 frames showing excellent temperature control with mean 94.73 K
First, basic checks. Figure 1a shows temperature fluctuating around 94.4 K—exactly what we want. Mean temperature was 94.73 K (just 0.33 K off target) with a standard deviation of 1.56 K. That’s better stability than Rahman achieved.
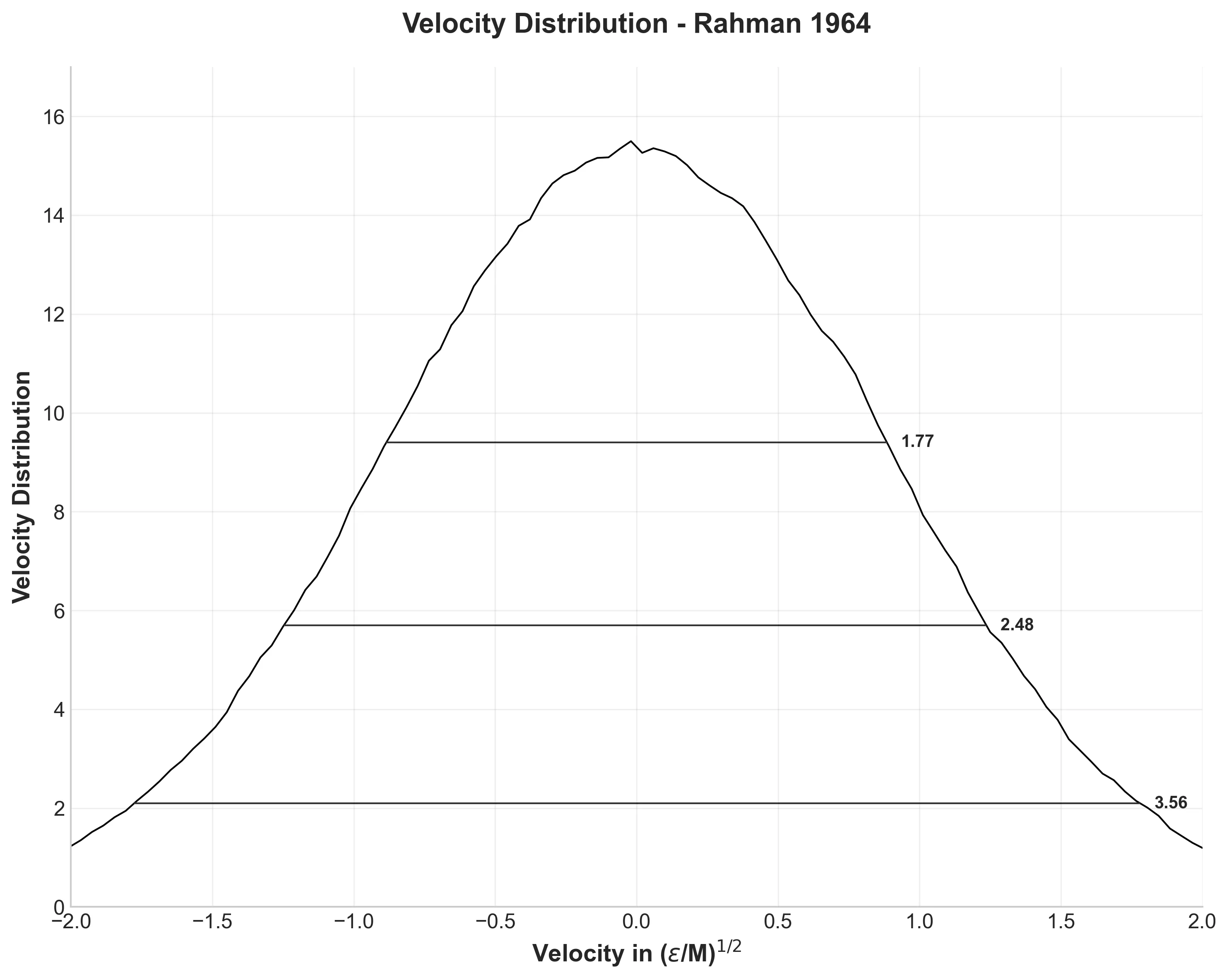
Maxwell-Boltzmann velocity distribution with measured distribution widths at various heights
Figure 1b shows the velocity distribution from 12.9 million velocity components. Perfect Maxwell-Boltzmann distribution, as expected for thermal equilibrium. The widths at various heights match Rahman’s results well: 1.77, 2.48, and 3.56 compared to his 1.77, 2.52, and 3.52.
Liquid Structure
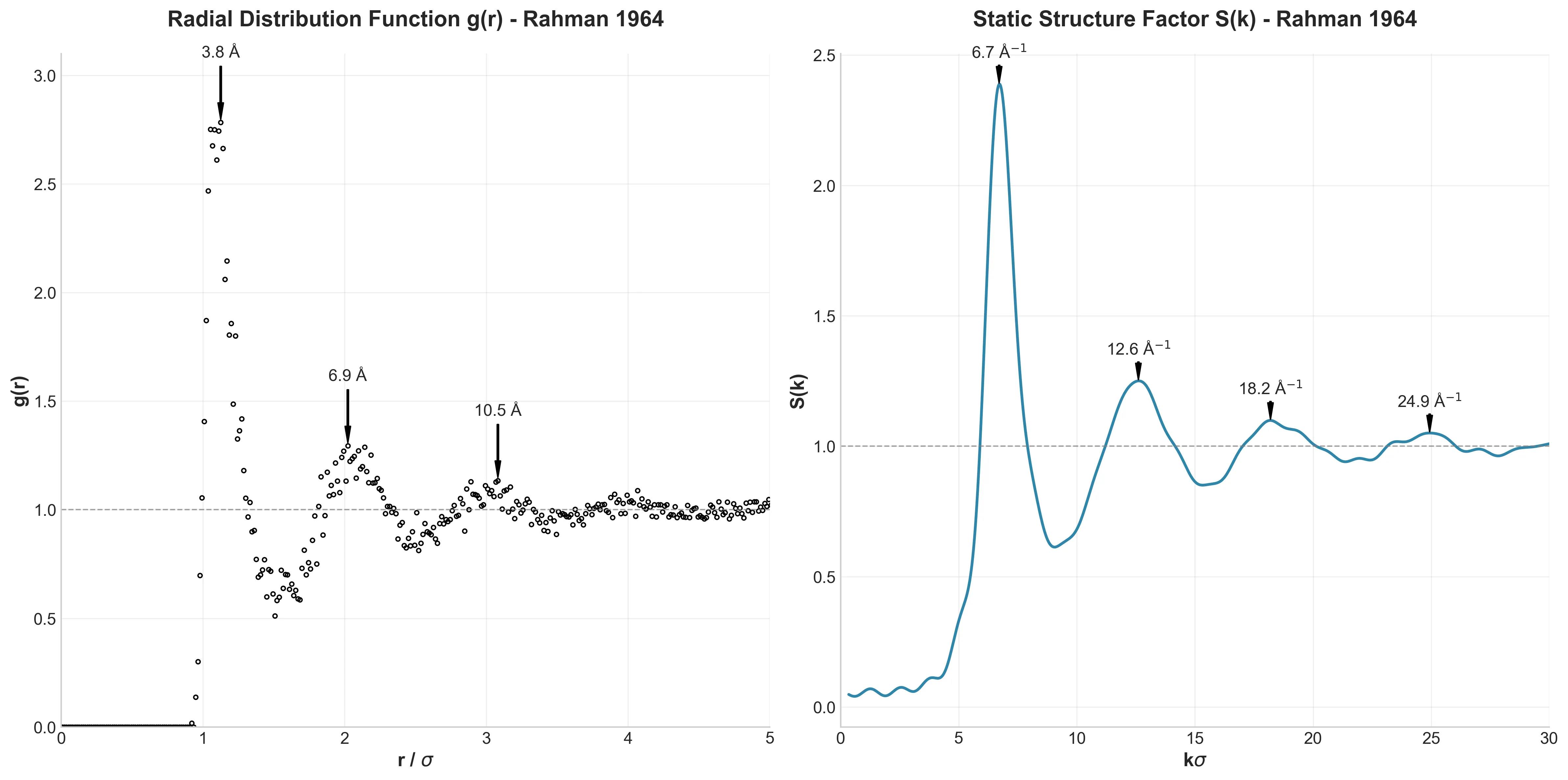
Left: Radial Distribution Function g(r) showing liquid structure; Right: Static Structure Factor S(k) with characteristic peaks
How are atoms arranged in a liquid? The Radial Distribution Function $g(r)$ (left panel) answers this. It shows the probability of finding another atom at distance $r$ from any reference atom.
The sharp first peak at 3.82 Å shows well-defined nearest neighbors, but subsequent peaks quickly dampen—that’s the liquid signature. Short-range order, long-range disorder. Rahman found the first peak at 3.7 Å; our 0.1 Å difference is negligible.
The Static Structure Factor $S(k)$ (right panel) is the Fourier transform of $g(r)$. This is what you’d measure in X-ray scattering experiments. Peak locations at 6.71, 12.6, 18.2, and 24.94 (in units of $k\sigma$) match Rahman’s expected values of 6.8, 12.5, 18.5, and 24.8 almost perfectly.
Diffusion: How Atoms Wander
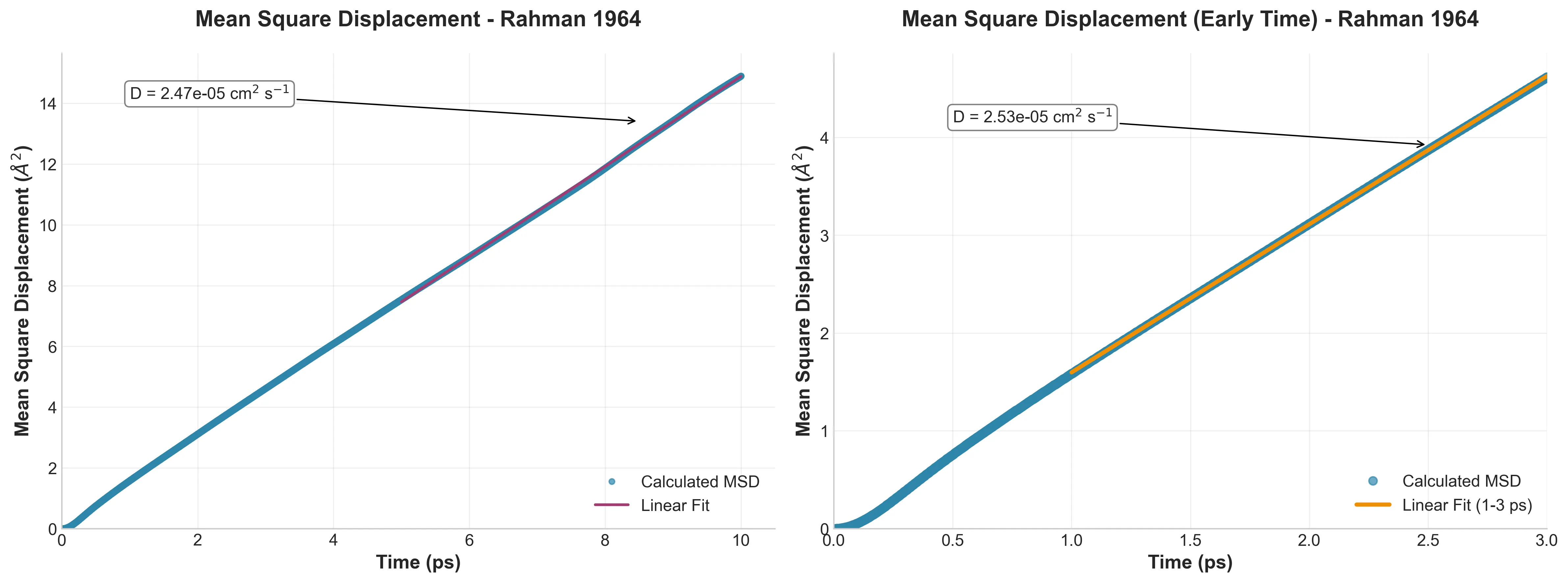
Mean Square Displacement vs. time showing ballistic to diffusive transition, with detailed early-time behavior (right panel)
Track how far atoms move over time and you get the Mean Square Displacement (MSD). Figure 3 shows the classic transition from ballistic motion (short times) to diffusive motion (linear regime).
The slope gives the diffusion coefficient: $D = 2.47 \times 10^{-5} \text{ cm}^2/\text{s}$ from my simulation versus Rahman’s $2.43 \times 10^{-5} \text{ cm}^2/\text{s}$. That’s 2% agreement after 60 years—not bad for completely different hardware and software.
The Cage Effect: Rahman’s Big Discovery
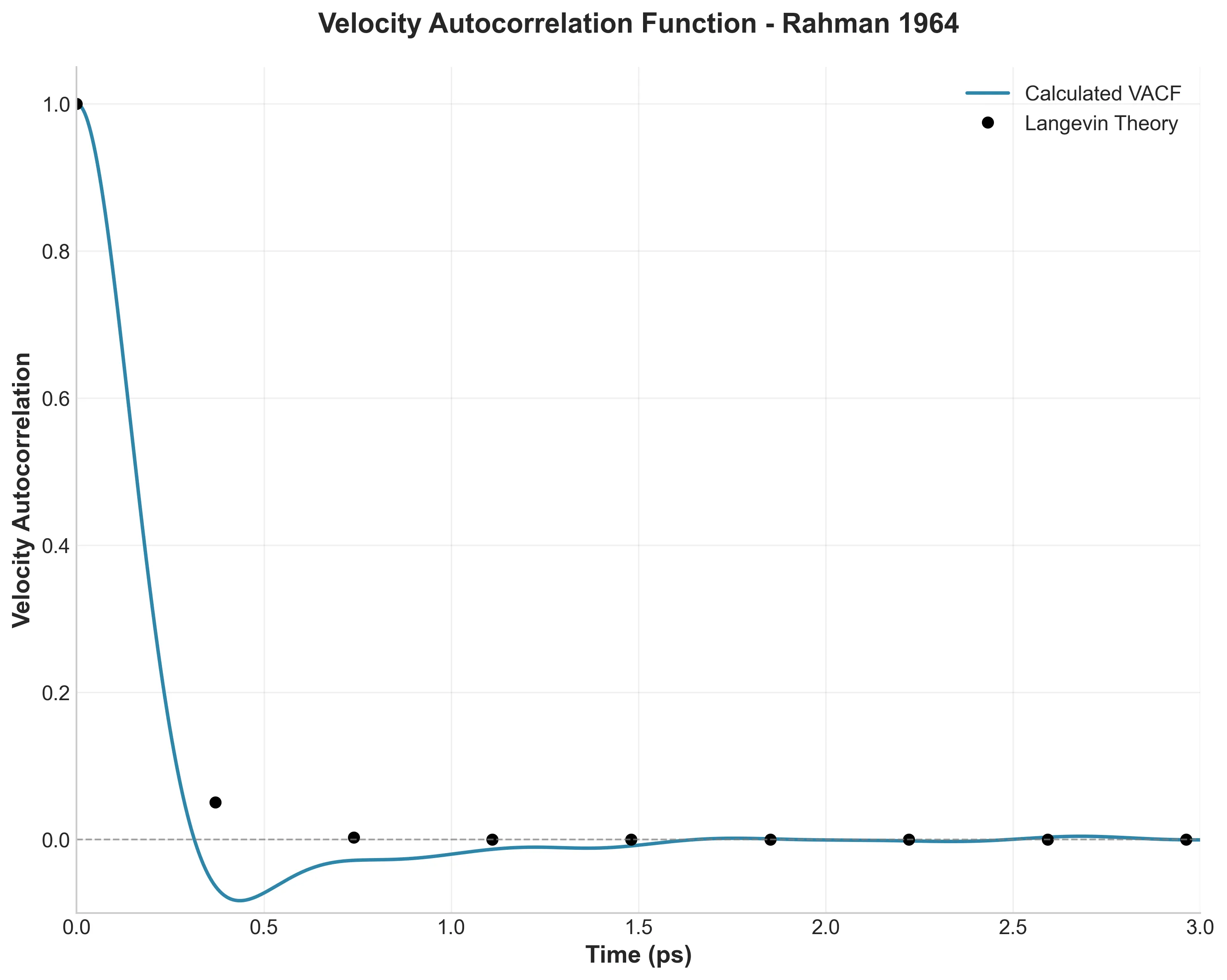
Velocity Autocorrelation Function showing the signature negative region characteristic of liquid dynamics
Here’s where Rahman made his most important discovery. The Velocity Autocorrelation Function (VACF) in Figure 4 measures how long an atom “remembers” its initial velocity.
In a gas, this would decay exponentially to zero. In Rahman’s liquid, something different happens: the VACF goes negative around 0.3 ps before slowly returning to zero. This is the “cage effect”—atoms get trapped by their neighbors and bounce backward.
My simulation captures this perfectly. The VACF reaches -0.020 at 1 ps, with a minimum of -0.083. This was Rahman’s key insight about liquid dynamics, and it’s still fundamental to how we understand liquids today.
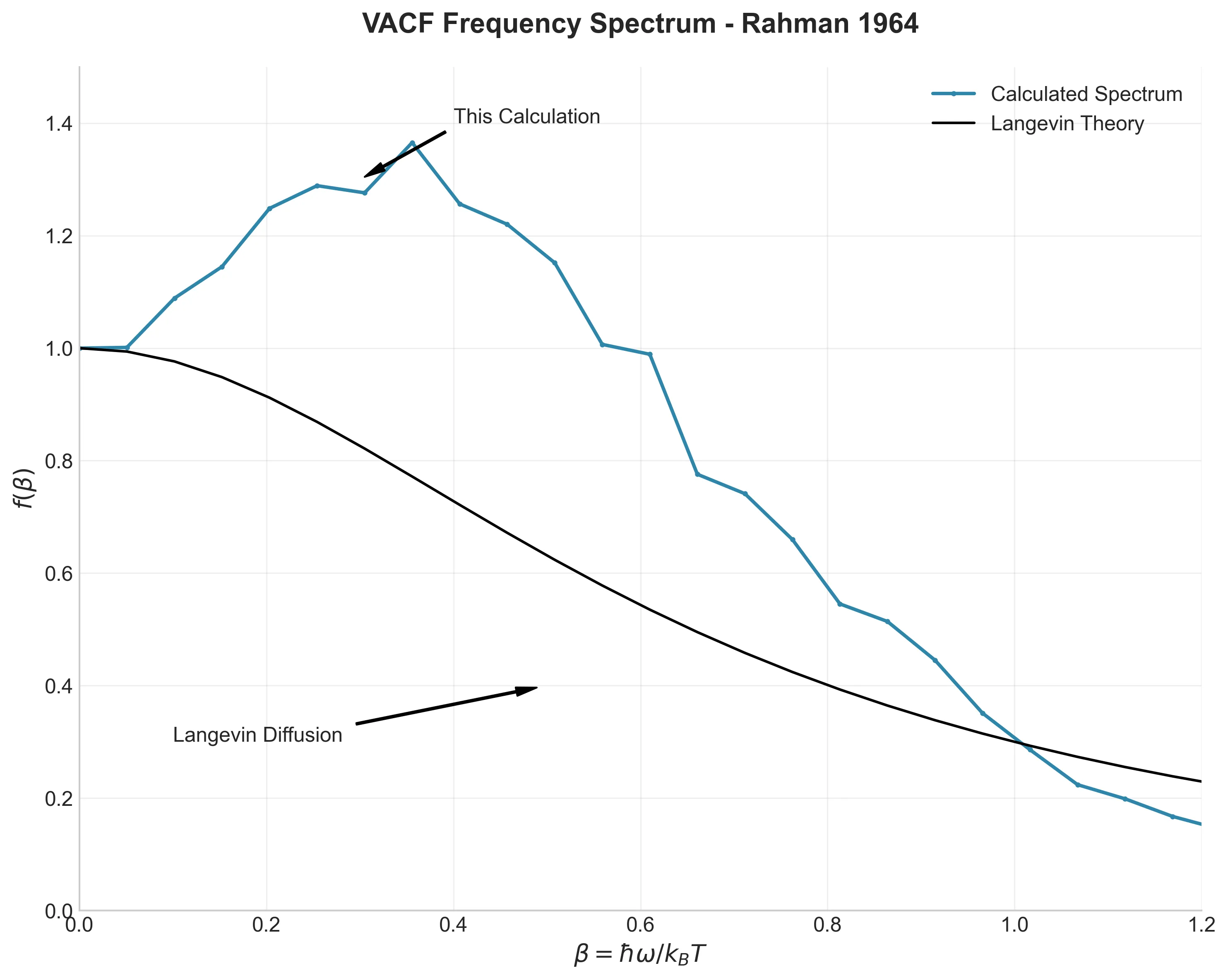
Frequency spectrum of the VACF showing characteristic peak from atomic caging effects
The Fourier transform of the VACF (Figure 5) shows something even more interesting. Instead of the simple curve predicted by diffusion theory, there’s a clear peak around $\beta = 0.25$ (where $\beta = \hbar\omega/k_B T$). This peak is atoms “rattling” in their cages—more like a solid than a gas. Rahman saw this too, and it became a key signature of liquid dynamics.
Advanced Analysis: Van Hove Functions
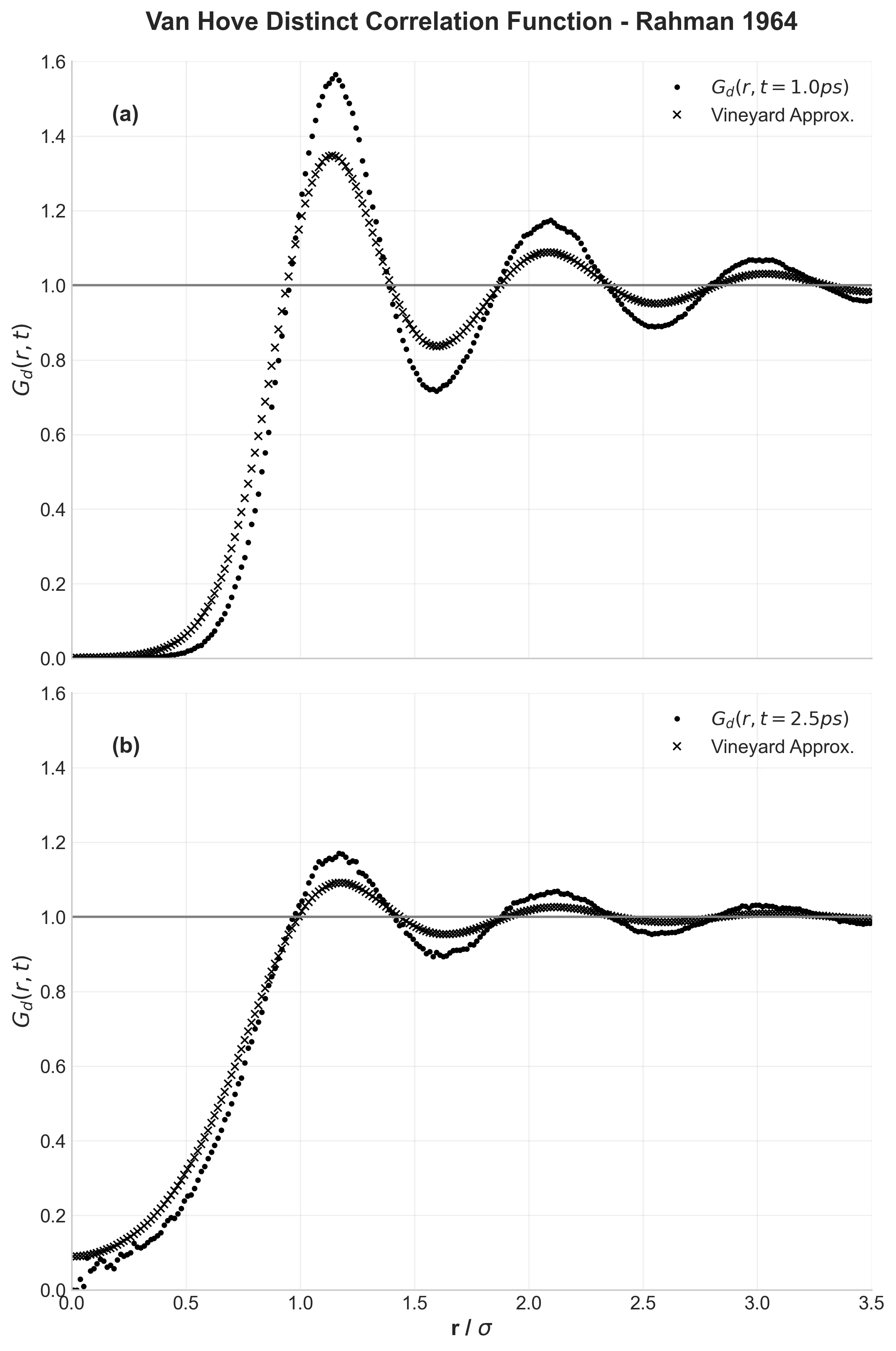
Van Hove distinct correlation function G_d(r,t) at two time points, showing evolution of liquid structure compared to Vineyard approximation
Rahman didn’t stop at basic properties. The Van Hove correlation function $G(r,t)$ describes how the liquid structure evolves over time. Figure 6 shows the distinct part—how neighbor shells “melt” as time progresses.
At 1.0 ps, the structure is still well-defined. By 2.5 ps, it’s more smeared out. Rahman compared this to theoretical predictions (the Vineyard approximation) and found the theory predicted too rapid decay. My results confirm this—the Vineyard approximation underestimates how persistent local structure is in liquids.
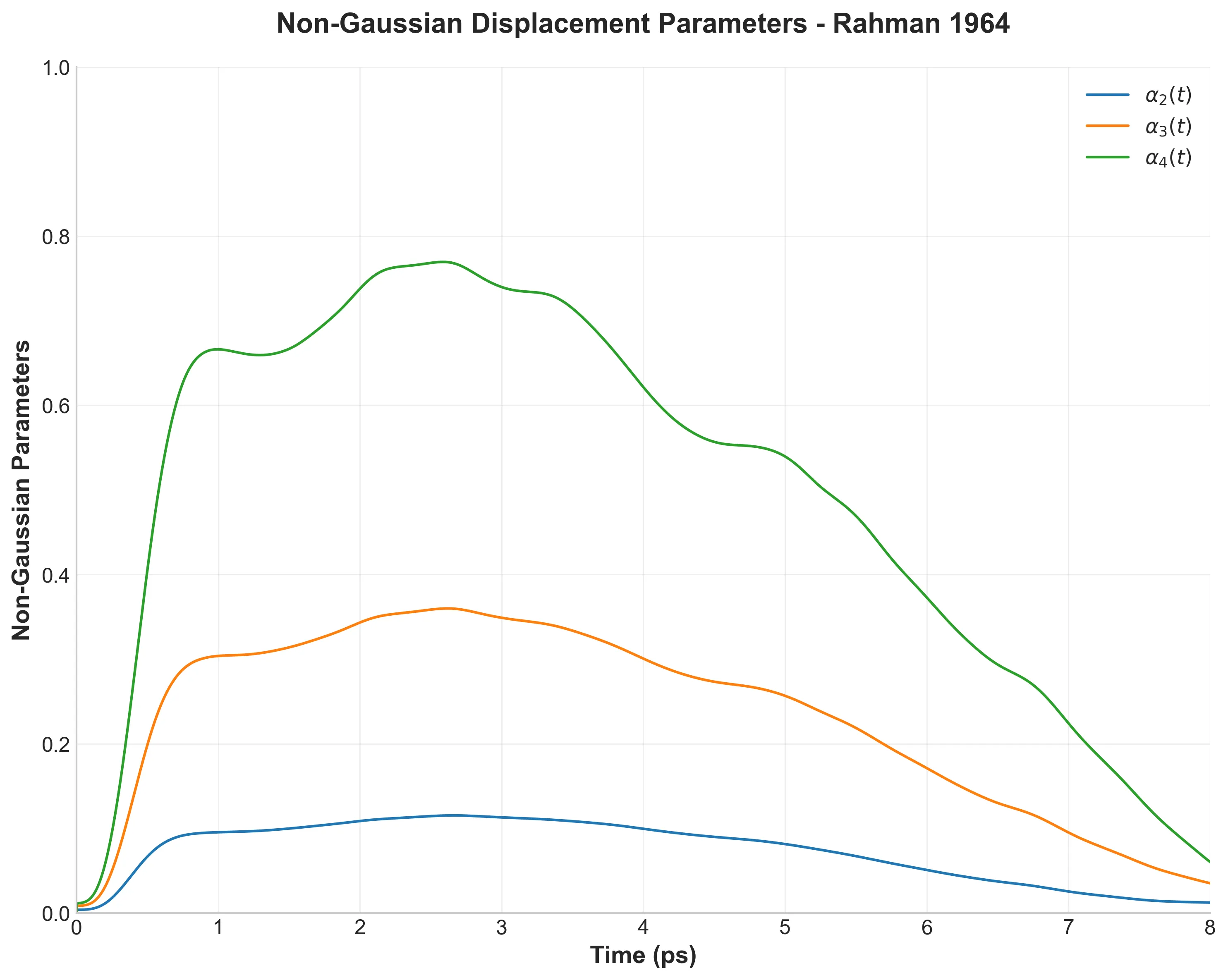
Non-Gaussian parameters α_n(t) showing deviation from simple diffusive behavior
Figure 7 shows that atomic motion isn’t simple random diffusion. The non-Gaussian parameters $\alpha_n(t)$ measure deviations from Gaussian behavior. If atoms moved via simple random walks, these would be zero.
Instead, they’re positive, with $\alpha_2$ reaching 0.115. This means some atoms make larger jumps while others stay more confined than expected. Rahman was the first to identify this non-Gaussian character in liquid dynamics.

Delayed convolution approximation testing Rahman’s theoretical improvement over the Vineyard approach
Figure 8 tests Rahman’s “delayed convolution approximation”—his proposed improvement over existing theory. By comparing actual structure evolution with theoretical predictions, this shows how simulation can validate and improve theoretical models. The delayed approach works better than the standard Vineyard method, demonstrating how computation and theory can work together.
Implementation Notes
Beyond reproducing the physics, this was an exercise in scientific software engineering:
- Clean architecture: Analysis code organized into a Python package (
src/argon_sim) with modules for thermodynamics, dynamics, and structure - Intelligent caching: Expensive calculations like MSD and VACF get cached to avoid recomputation
- Memory management: Large datasets processed in chunks to handle the 864 × 5001 atom-frame matrices efficiently
- Reproducibility: A
Makefilelets you install dependencies, run simulations, and generate every figure with simple commands
What took Rahman months on an IBM mainframe now runs in less than an hour on a laptop, with better numerical accuracy and statistical precision.
Why This Still Matters
Replicating Rahman’s work was more than a nostalgia trip. The quantitative agreement is striking: diffusion coefficients within 2%, structural peaks within 0.1 Å, velocity distributions matching to three significant figures.
This level of reproducibility, achieved with completely different hardware and software, validates something profound. Rahman’s physical model was fundamentally sound—the Lennard-Jones potential captures liquid argon physics with extraordinary fidelity. His computational methods, while limited by 1960s technology, were methodologically rigorous.
Most importantly, Rahman didn’t just simulate a liquid—he created the conceptual framework for modern computational materials science. Molecular dynamics has grown from 864 atoms to millions, but the core insight remains: Newton’s equations plus statistical mechanics equals a window into the atomic world.
This replication shows that some physics is universal. The cage effect, the velocity correlations, the structural evolution—these aren’t artifacts of 1960s computing. They’re fundamental features of how matter behaves at the atomic scale.