Beyond Direct Encoding
NEAT evolved networks through direct encoding (each gene explicitly specified nodes and connections). While elegant for small networks, this approach hits a wall with larger architectures. Evolving networks with billions of connections like the brain requires a fundamentally different approach.
HyperNEAT introduces indirect encoding through geometric principles. Instead of specifying every connection explicitly, HyperNEAT evolves patterns that generate connections based on spatial relationships. This enables evolution of large networks with biological regularities: symmetry, repetition, and locality.
The key insight is leveraging Compositional Pattern Producing Networks (CPPNs) to map coordinates to connection weights, exploiting the geometric organization found in natural neural networks.
HyperNEAT: The Core Algorithm
Biological Motivation
The human brain exhibits remarkable organizational principles that typical artificial neural networks lack:
- Scale: ~86 billion neurons with ~100 trillion connections
- Repetition: Structural patterns reused across regions
- Symmetry: Mirrored structures like bilateral visual processing
- Locality: Spatial proximity influences connectivity and function
Standard neural networks, whether hand-designed or evolved through NEAT, rarely exhibit these properties. Dense feedforward layers connect every node to every other, creating unstructured connectivity patterns that waste parameters and miss important spatial relationships.
HyperNEAT aims to evolve networks that capture these biological regularities, potentially leading to more efficient and interpretable architectures.
Compositional Pattern Producing Networks
CPPNs are the foundation of HyperNEAT’s indirect encoding. Think of them as pattern generators that create complex spatial structures from simple coordinate inputs.
Biological Inspiration
DNA exemplifies indirect encoding (roughly 30,000 genes specify a brain with trillions of connections). This massive compression ratio suggests that simple rules can generate complex structures through developmental processes.
CPPNs abstract this concept, using compositions of mathematical functions to create patterns in coordinate space. The same “genetic” program (function composition) can be reused across different locations and scales, just like how developmental genes control pattern formation throughout an organism.
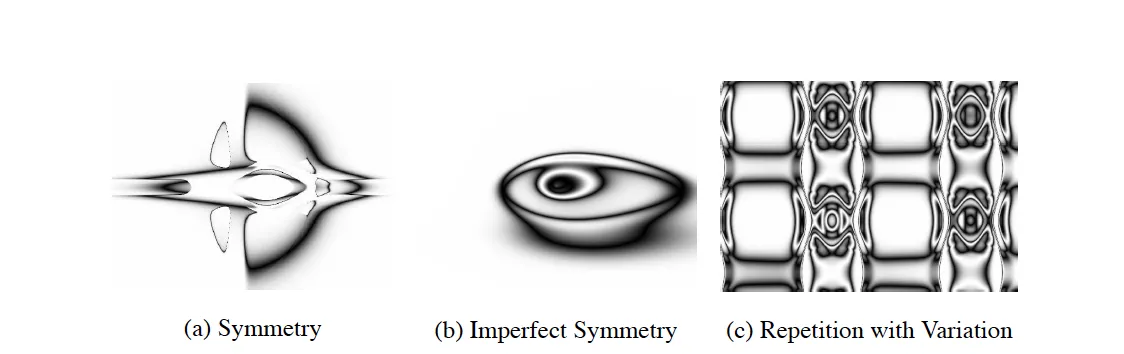
Pattern Generation Through Function Composition
CPPNs generate patterns by composing simple mathematical functions. Key function types include:
- Gaussian functions: Create symmetric patterns and gradients
- Trigonometric functions: Generate periodic/repetitive structures
- Linear functions: Produce gradients and asymmetric patterns
- Sigmoid functions: Create sharp transitions and boundaries
By combining these functions, CPPNs can encode complex regularities that would require many explicit rules in direct encoding.
Evolution of CPPNs
HyperNEAT uses NEAT to evolve the CPPN structure rather than the final neural network directly. This brings several advantages:
- Complexification: CPPNs start simple and grow more complex only when beneficial
- Historical markings: Enable proper crossover between different CPPN topologies
- Speciation: Protects innovative CPPN patterns during evolution
Additional activation functions beyond standard neural networks are crucial:
- Gaussian functions for symmetry
- Sine/cosine for repetition
- Specialized functions for specific geometric patterns
The HyperNEAT Process
Substrates: Geometric Organization
A substrate defines the spatial arrangement of neurons. Unlike traditional networks where connectivity follows layer-based rules, substrates embed neurons in geometric space (2D grids, 3D volumes, etc.).
The CPPN maps from coordinates to connection weights:
$$\text{CPPN}(x_1, y_1, x_2, y_2) = w$$
Where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of two neurons, and $w$ determines their connection weight.
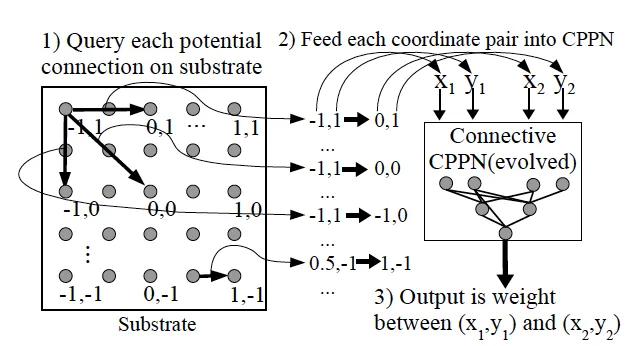
This geometric approach enables several key properties:
- Locality: Nearby neurons tend to have similar connectivity patterns
- Symmetry: Patterns can be mirrored across spatial axes
- Repetition: Periodic functions create repeating motifs
- Scalability: The same pattern can be applied at different resolutions
Emergent Regularities
The geometric encoding naturally produces the desired biological patterns:
Symmetry emerges from symmetric functions. A Gaussian centered at the origin creates identical patterns when $(x_1, y_1)$ and $(x_2, y_2)$ are equidistant from the center.
Repetition arises from periodic functions like sine and cosine. These create repeating connectivity motifs across the substrate.
Locality results from functions that vary smoothly across space. Nearby coordinates produce similar outputs, leading to local connectivity patterns.
Imperfect regularity occurs when these patterns are modulated by additional coordinate dependencies, creating biological-like variation within the basic structure.
Substrate Configurations
The choice of substrate geometry critically influences network behavior. Several standard configurations exist:
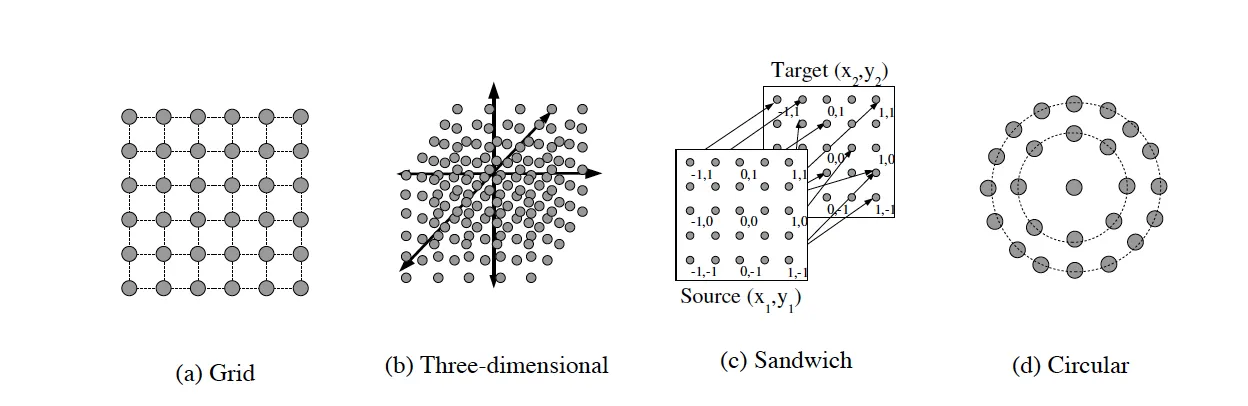
2D Grid: Simple planar arrangement, CPPN takes four coordinates $(x_1, y_1, x_2, y_2)$
3D Volume: Extends to three dimensions, CPPN becomes six-dimensional $(x_1, y_1, z_1, x_2, y_2, z_2)$
Sandwich: Input layer connects only to output layer, useful for sensory-motor tasks
Circular: Radial geometry enables rotation-invariant patterns and cyclic behaviors
The substrate must be chosen before evolution begins, making domain knowledge important for success.
Exploiting Input-Output Geometry
Unlike traditional networks that treat inputs as abstract vectors, HyperNEAT can exploit the spatial organization of inputs and outputs. For visual tasks, pixel coordinates provide meaningful geometric information. For control problems, sensor and actuator layouts can guide connectivity patterns.

This spatial awareness allows HyperNEAT to:
- Develop receptive fields similar to biological vision systems
- Create locally connected patterns for spatial processing
- Generate symmetric motor control patterns
- Scale across different input resolutions
Resolution Independence
A unique advantage of HyperNEAT is substrate resolution independence. Networks evolved on low-resolution substrates can be deployed on higher-resolution versions without retraining. The CPPN’s coordinate-based mapping scales naturally across different granularities.
This property suggests that evolved patterns capture fundamental spatial relationships rather than memorizing specific connectivity patterns, a key insight for scalable neural architecture design.
Complete Algorithm
The HyperNEAT process:
- Define substrate geometry: Choose spatial arrangement and input/output locations
- Initialize CPPN population: Create minimal networks using NEAT initialization
- For each generation:
- Generate neural networks by querying each CPPN with coordinate pairs
- Evaluate network performance on the target task
- Evolve CPPNs using NEAT (selection, mutation, crossover, speciation)
- Return best network: Deploy the highest-performing network architecture
Impact and Future Directions
HyperNEAT demonstrated that indirect encoding could evolve large neural networks with biological regularities. The algorithm’s key insights, exploiting geometry, generating patterns through function composition, and scaling across resolutions, continue to influence modern research.
Extensions like ES-HyperNEAT add even more sophisticated capabilities by evolving the substrate itself. As neural architecture search becomes increasingly important, HyperNEAT’s principles find new applications in hybrid approaches that combine evolutionary pattern generation with gradient-based optimization.
The algorithm’s emphasis on spatial organization and regularity also connects to contemporary work on geometric deep learning and equivariant networks, suggesting that evolution and hand-design may converge on similar organizing principles for building structured, efficient neural architectures.
