Automating Neural Architecture Design
Designing neural network architectures is typically a manual, iterative process. Researchers experiment with different layer configurations, activation functions, and connection patterns, often guided by intuition and empirical results. Evolution offers an automated alternative to this design process.
NEAT (NeuroEvolution of Augmenting Topologies) introduced a compelling answer in 2002. This algorithm optimizes network weights and evolves the network structure itself, starting from minimal topologies and growing complexity only when beneficial.
NEAT’s core innovations solved fundamental problems that had plagued earlier attempts at topology evolution. Its solutions for genetic encoding, structural crossover, and innovation protection remain influential today, especially as neural architecture search and automated ML gain prominence.
The Core Challenges of NEAT
Evolving neural network topologies presents several fundamental challenges that NEAT elegantly addressed. Understanding these problems helps explain why NEAT’s solutions were so influential.
Genetic Encoding: How to Represent Networks
Evolutionary algorithms require a genetic representation, a way to encode individuals that enables meaningful selection, mutation, and crossover. For neural networks, this choice is critical.
Direct encoding explicitly represents each network component. Genes directly correspond to nodes and connections. This approach is intuitive and readable, and it works well for smaller networks.
Indirect encoding specifies construction rules or processes. These encodings are more compact and can generate highly complex structures from simple rules.
NEAT chose direct encoding with a simple two-part structure: separate gene lists for nodes and connections. This balances simplicity with the flexibility needed for evolutionary operations.
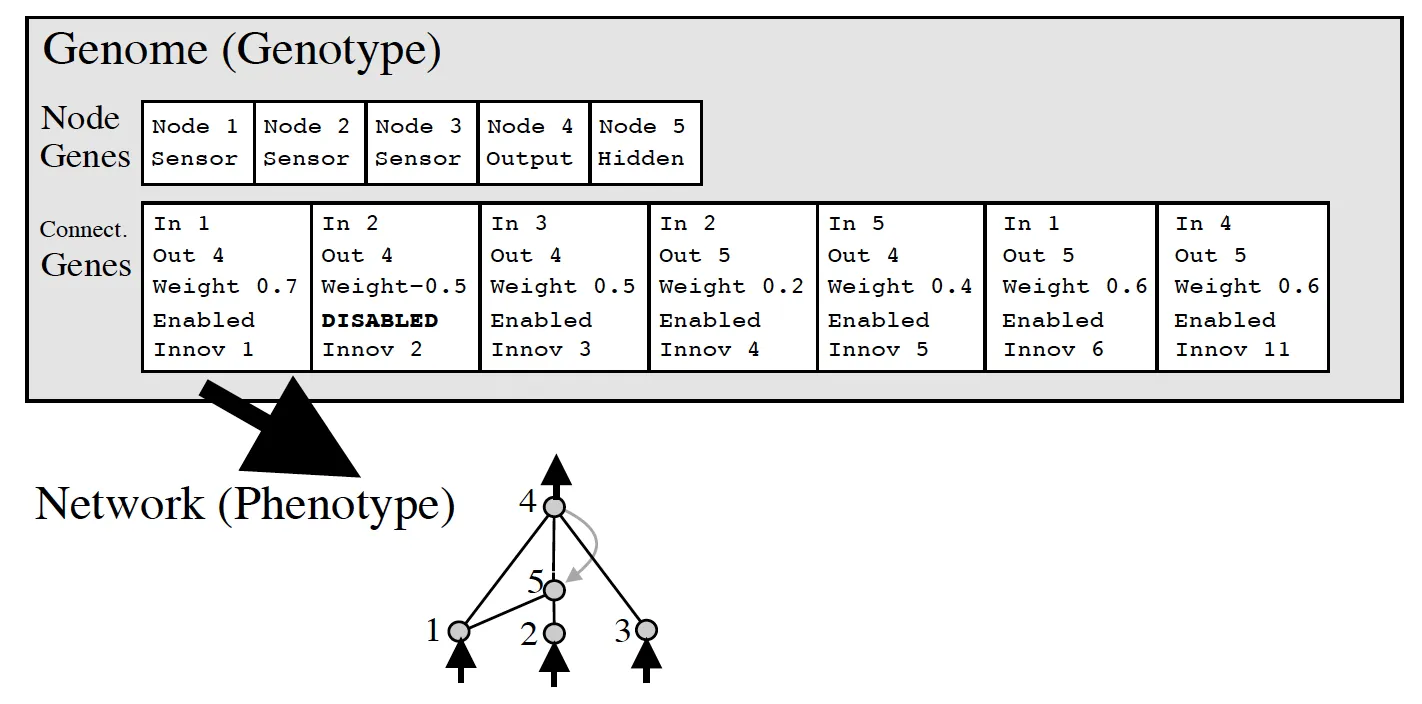
Connection genes specify the source and target nodes, weight, enabled status, and an innovation number for historical tracking. Input and output nodes are fixed; only hidden nodes evolve.
Structural Mutations: Growing Complexity
NEAT employs two categories of mutations to evolve both weights and structure:
Weight mutations adjust existing connection strengths using standard perturbation methods, the familiar approach from traditional neuroevolution.
Structural mutations add new network components:
- Add connection: Creates a new link between existing nodes with a random initial weight
- Add node: Splits an existing connection by inserting a new node. The original connection is disabled, while two new connections replace it. One inherits the original weight, the other starts at 1.0
This node-splitting approach minimizes disruption. The new node initially acts as an identity function, giving it time to prove useful before natural selection pressure intensifies.
Solving the Competing Conventions Problem
Performing crossover between networks with different structures presents a fundamental challenge. Consider two networks that solve the same problem using different internal organizations. Naive crossover between them typically produces broken offspring.
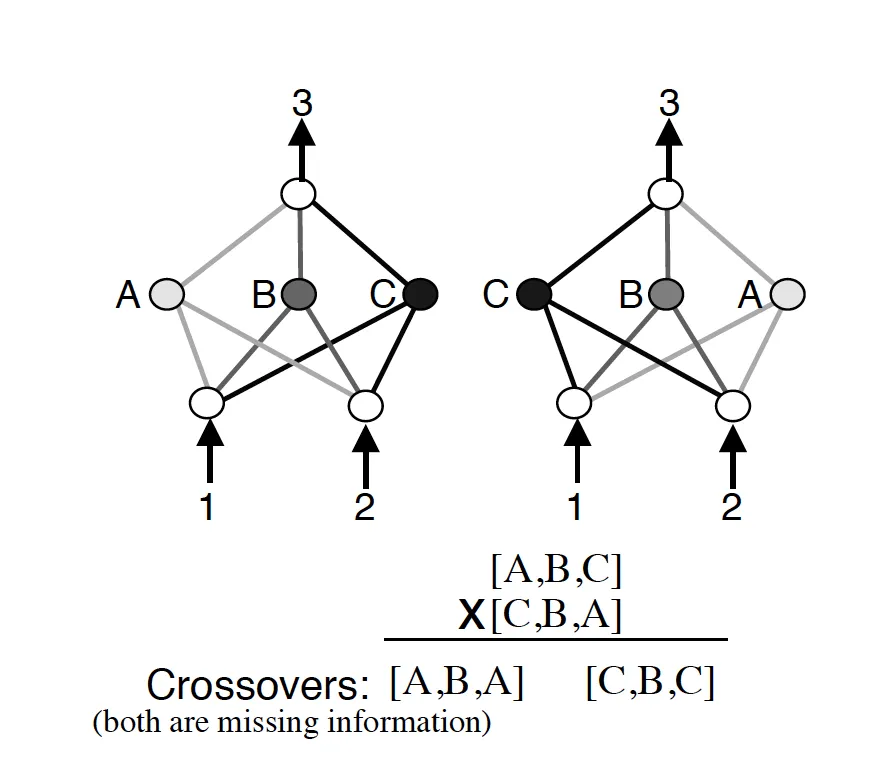
NEAT’s solution draws inspiration from biology through historical markings. Each structural innovation (adding a node or connection) receives a unique innovation number, a timestamp of when that change first appeared in the population.
During crossover, genes with matching innovation numbers are aligned and combined. This biological concept of homology enables meaningful recombination between networks of different sizes and structures.
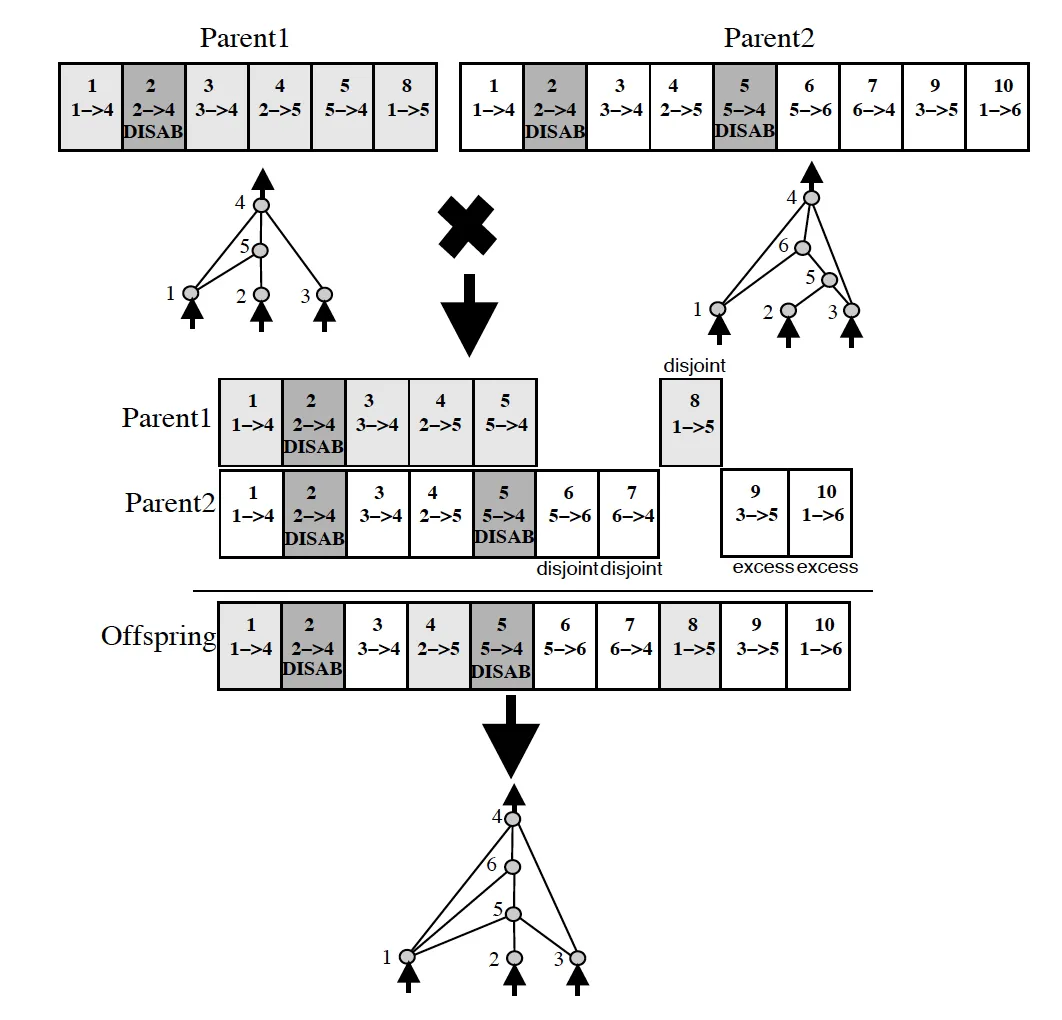
Protecting Innovation Through Speciation
New structural innovations face a harsh reality: they usually perform worse initially. Adding nodes or connections typically decreases performance before optimization can improve the new structure. Without protection, these innovations disappear before realizing their potential.
NEAT addresses this through speciation: dividing the population into species based on structural and weight similarity. The historical markings that enable crossover also measure compatibility between individuals.
Crucially, individuals only compete within their species. This gives new structural innovations time to optimize without immediately competing against established, well-tuned networks.
Explicit fitness sharing enhances this protection: species divide their collective fitness among members, preventing any single species from dominating the population while maintaining diversity for continued exploration.
Complexification: Starting Minimal
NEAT begins with the simplest possible networks (just input and output nodes connected by random weights). No hidden layers exist initially. Complexity emerges only when mutations that add structure prove beneficial.
This complexification approach builds efficient solutions that solve problems with minimal structure. Combined with speciation, it tends to produce highly optimized architectures.
Scaling Up: HyperNEAT
NEAT evolved networks through direct encoding, where each gene explicitly specifies nodes and connections. Scaling this approach to larger architectures requires a fundamentally different method. Evolving networks with billions of connections like the brain requires indirect encoding.
HyperNEAT introduces indirect encoding through geometric principles. HyperNEAT evolves geometric patterns that generate connections based on spatial relationships. This enables the evolution of large networks with biological regularities: symmetry, repetition, and locality.
The key insight is leveraging Compositional Pattern Producing Networks (CPPNs) to map coordinates to connection weights, exploiting the geometric organization found in natural neural networks.
Biological Motivation
The human brain exhibits remarkable organizational principles:
- Scale: ~86 billion neurons with ~100 trillion connections
- Repetition: Structural patterns reused across regions
- Symmetry: Mirrored structures like bilateral visual processing
- Locality: Spatial proximity influences connectivity and function
HyperNEAT aims to evolve networks that capture these biological regularities, leading to more efficient and interpretable architectures.
Compositional Pattern Producing Networks
CPPNs are the foundation of HyperNEAT’s indirect encoding. Think of them as pattern generators that create complex spatial structures from simple coordinate inputs.
DNA exemplifies indirect encoding (roughly 30,000 genes specify a brain with trillions of connections). This massive compression ratio suggests that simple rules can generate complex structures through developmental processes.
CPPNs abstract this concept, using compositions of mathematical functions to create patterns in coordinate space. The same genetic program (function composition) can be reused across different locations and scales, just like how developmental genes control pattern formation throughout an organism.
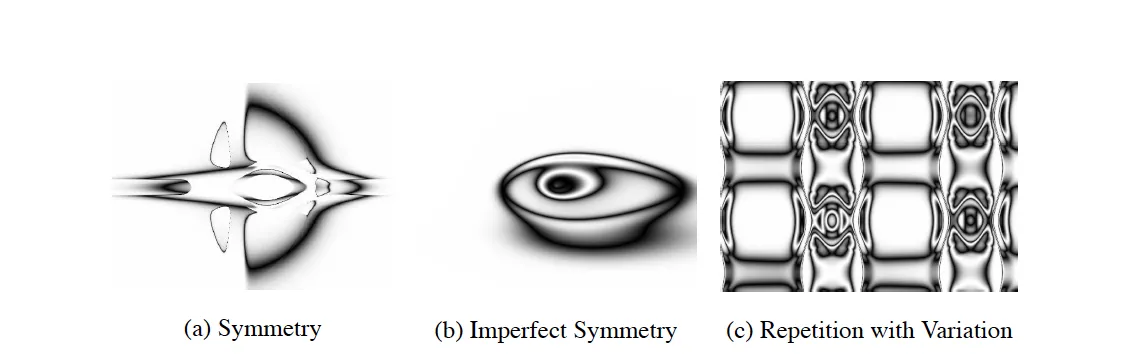
Pattern Generation Through Function Composition
CPPNs generate patterns by composing simple mathematical functions. Key function types include:
- Gaussian functions: Create symmetric patterns and gradients
- Trigonometric functions: Generate periodic/repetitive structures
- Linear functions: Produce gradients and asymmetric patterns
- Sigmoid functions: Create sharp transitions and boundaries
By combining these functions, CPPNs can encode complex regularities that would require many explicit rules in direct encoding.
Evolution of CPPNs
HyperNEAT uses NEAT to evolve the CPPN structure. This brings several advantages:
- Complexification: CPPNs start simple and grow more complex only when beneficial
- Historical markings: Enable proper crossover between different CPPN topologies
- Speciation: Protects innovative CPPN patterns during evolution
Additional activation functions beyond standard neural networks are crucial:
- Gaussian functions for symmetry
- Sine/cosine for repetition
- Specialized functions for specific geometric patterns
The HyperNEAT Process
Substrates: Geometric Organization
A substrate defines the spatial arrangement of neurons. Substrates embed neurons in geometric space (2D grids, 3D volumes, etc.), providing an alternative to layer-based connectivity rules.
The CPPN maps from coordinates to connection weights:
$$\text{CPPN}(x_1, y_1, x_2, y_2) = w$$
Where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of two neurons, and $w$ determines their connection weight.
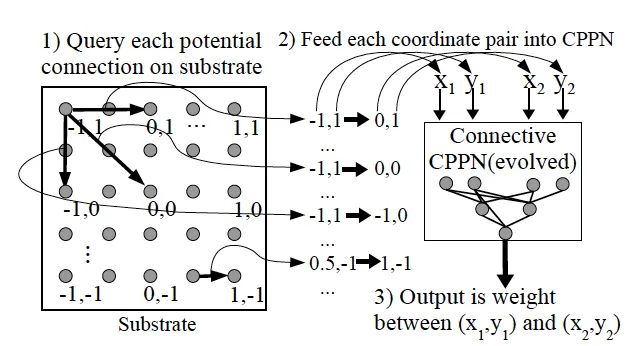
This geometric approach enables several key properties:
- Locality: Nearby neurons tend to have similar connectivity patterns
- Symmetry: Patterns can be mirrored across spatial axes
- Repetition: Periodic functions create repeating motifs
- Scalability: The same pattern can be applied at different resolutions
Emergent Regularities
The geometric encoding naturally produces the desired biological patterns:
Symmetry emerges from symmetric functions. A Gaussian centered at the origin creates identical patterns when $(x_1, y_1)$ and $(x_2, y_2)$ are equidistant from the center.
Repetition arises from periodic functions like sine and cosine. These create repeating connectivity motifs across the substrate.
Locality results from functions that vary smoothly across space. Nearby coordinates produce similar outputs, leading to local connectivity patterns.
Imperfect regularity occurs when these patterns are modulated by additional coordinate dependencies, creating biological-like variation within the basic structure.
Substrate Configurations
The choice of substrate geometry critically influences network behavior. Several standard configurations exist:
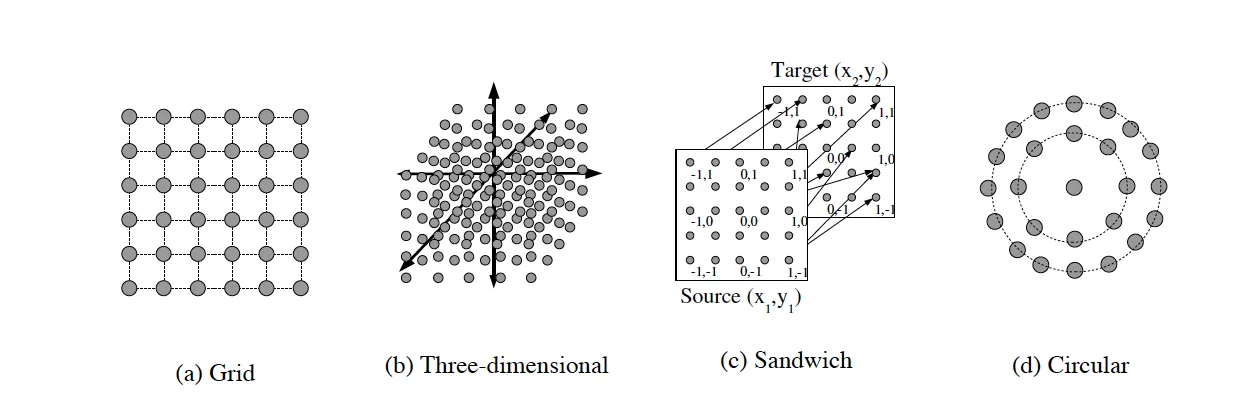
2D Grid: Simple planar arrangement, CPPN takes four coordinates $(x_1, y_1, x_2, y_2)$
3D Volume: Extends to three dimensions, CPPN becomes six-dimensional $(x_1, y_1, z_1, x_2, y_2, z_2)$
Sandwich: Input layer connects only to output layer, useful for sensory-motor tasks
Circular: Radial geometry enables rotation-invariant patterns and cyclic behaviors
The substrate must be chosen before evolution begins, making domain knowledge important for success.
Exploiting Input-Output Geometry
HyperNEAT exploits the spatial organization of inputs and outputs. For visual tasks, pixel coordinates provide meaningful geometric information. For control problems, sensor and actuator layouts can guide connectivity patterns.
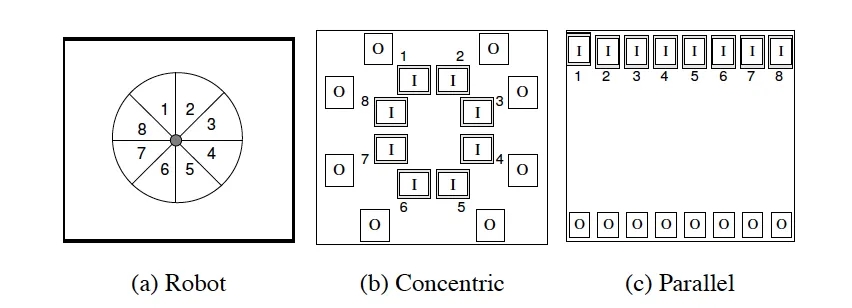
This spatial awareness allows HyperNEAT to:
- Develop receptive fields similar to biological vision systems
- Create locally connected patterns for spatial processing
- Generate symmetric motor control patterns
- Scale across different input resolutions
Resolution Independence
A unique advantage of HyperNEAT is substrate resolution independence. Networks evolved on low-resolution substrates can be deployed on higher-resolution versions without retraining. The CPPN’s coordinate-based mapping scales naturally across different granularities.
This property suggests that evolved patterns capture fundamental spatial relationships, providing a key insight for scalable neural architecture design.
Impact and Future Directions
NEAT and HyperNEAT demonstrated that evolution could design neural network topologies and scale them through indirect encoding. The algorithms’ key insights, exploiting geometry, generating patterns through function composition, and scaling across resolutions, continue to influence modern research.
Extensions like ES-HyperNEAT add even more sophisticated capabilities by evolving the substrate itself. As neural architecture search becomes increasingly important, these principles find new applications in hybrid approaches that combine evolutionary pattern generation with gradient-based optimization.
The emphasis on spatial organization and regularity also connects to contemporary work on geometric deep learning and equivariant networks, suggesting that evolution and hand-design converge on similar organizing principles for building structured, efficient neural architectures.
