Introduction
During my graduate studies, I came across many ways of representing molecular structure–so called molecular descriptors–that are useful for machine learning. Today, I want to talk about one of these representations: the Coulomb matrix [1].
A key goal when applying machine learning to atomistic problems is to go from a 3D molecular structure to some property of interest, such as the atomization energy or the dipole moment. The issue is that the 3D structure of a molecule isn’t directly what we want to use for machine learning. Why is that?
Scalar properties of interest (like energy) are not sensitive to the absolute position of the atoms in space. Instead, they have rotation and translation invariance: if we rotate or translate the molecule, the property of interest doesn’t change. Additionally, we don’t want our machine learning model to be sensitive to the indexing of the atoms (e.g., the order in which they are listed in a file, permutation invariance).
Clearly, Cartesian coordinates don’t have these invariants, so we need to transform them into a more suitable representation for machine learning. If we don’t do this, our machine learning model will have to learn these invariants from the data, which is inefficient being as they’re already known a priori. Wouldn’t it be better to focus on learning what we don’t already know?
The Coulomb Matrix
The Coulomb matrix is a molecular descriptor that is invariant to translation and rotation. It was first introduced in 2012 by Rupp et al. [1] and has since been widely used in the field of machine learning for molecules, although there are many more advanced representations available today [2].
For a molecule with $N$ atoms, the Coulomb matrix is a symmetric $N \times N$ matrix, where the element $C_{ij}$ is given by
$$ C_{ij} = \begin{cases} 0.5 Z_i^{2.4} & \text{if } i = j, \\ \frac{Z_i Z_j}{|\mathbf{R}_i - \mathbf{R}_j|} & \text{if } i \neq j, \end{cases} $$
where $Z_i$ is the atomic number of atom $i$, and $\mathbf{R}_i$ is the position of atom $i$ in 3D space. The diagonal elements come from fitting a relationship between the atomic number and total energy of an atom, and the off-diagonal elements mimic the pairwise Coulombic interactions between atoms [3].
Some things to note about the Coulomb matrix:
- It is invariant to translation and rotation.
- It is a symmetric matrix.
- It describes the global structure of the molecule, in contrast with local representations like the bag-of-bonds or the bag-of-angles.
- It captures the 3D shape of the molecule.
Let’s see what that looks like in practice.
Example: Bicyclobutane
Let’s calculate the Coulomb matrix for Bicyclobutane.
Bicyclobutane (Smokefoot, Public domain, via Wikimedia Commons)
This molecule is kind of interesting. Its structure is very strained, but it’s stable enough to be isolated and studied.
We’ll interact with bicyclobutane using the following Python libraries:
from ase.build import molecule
from ase.visualize import view
# Create the molecule
bicyclobutane = molecule('bicyclobutane')
# Visualize the molecule
view(bicyclobutane, viewer='x3d')
As an output, you should see a 3D visualization of the molecule.
Bicyclobutane
Now, let’s calculate the Coulomb matrix.
from dscribe.descriptors import CoulombMatrix
# Setting up the CM descriptor
cm = CoulombMatrix(n_atoms_max=len(bicyclobutane))
# Create CM output for the system
cm_bicyclobutane = cm.create(bicyclobutane)
cm_bicyclobutane = cm_bicyclobutane.reshape(len(bicyclobutane), len(bicyclobutane))
The Coulomb matrix is a symmetric matrix, so we can visualize it as a heatmap.
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8), dpi=150)
plt.imshow(cm_bicyclobutane, cmap='coolwarm')
plt.colorbar(label='magnitude')
plt.title('Coulomb Matrix for Bicyclobutane')
plt.show()
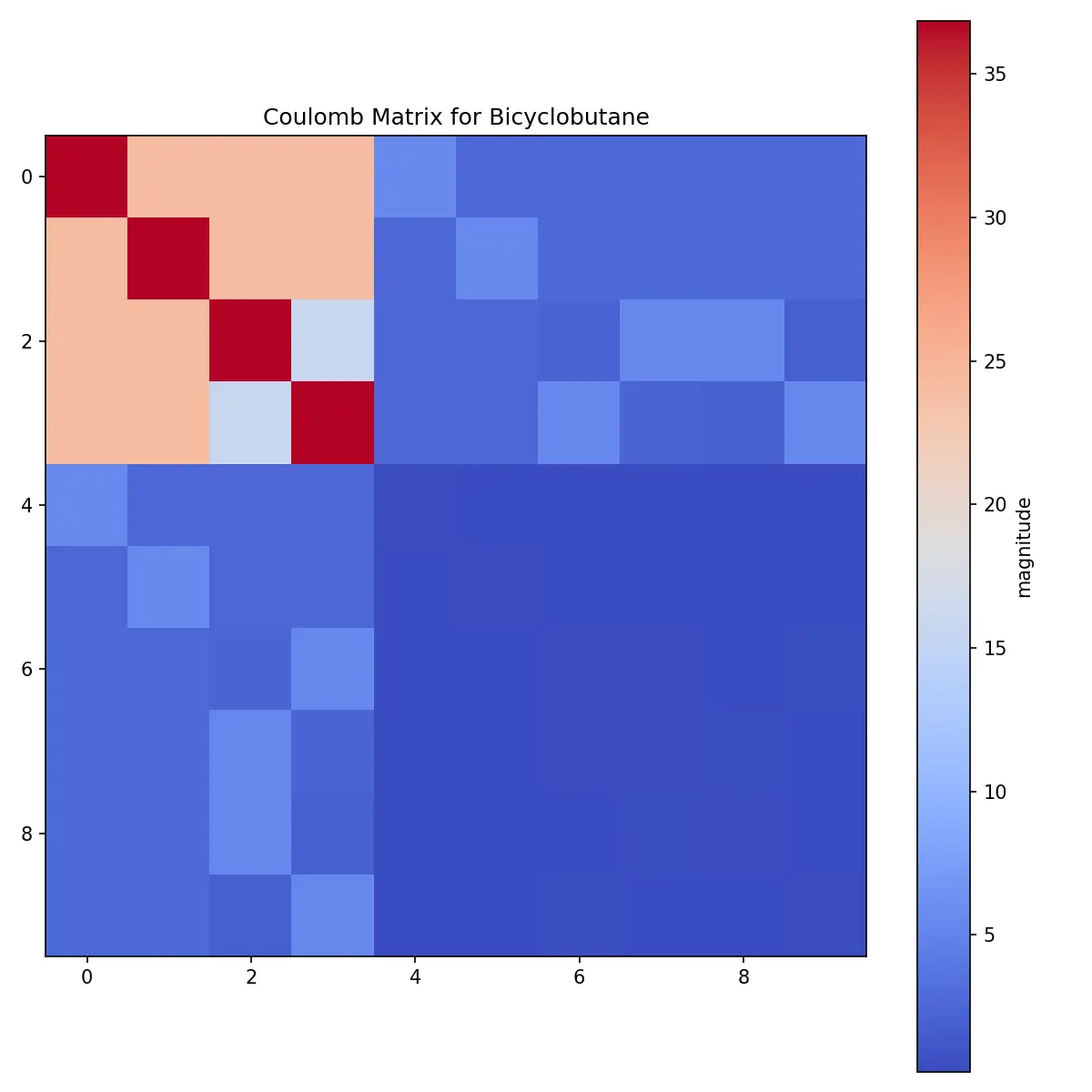
Coulomb matrix of Bicyclobutane
What can we observe from the Coulomb matrix?
- We see the heavy carbon atoms in the upper left
- Diagonal elements are large, indicating the self-interaction of the atoms
- The off-diagonal elements are small, indicating the weak interaction between the atoms
- Two carbons are close to three carbons, and the others have a slightly larger distance with its neighbors
- The hydrogen atoms barely contribute to the Coulomb matrix
In fact, as a positive definite matrix, it might be more informative to visualize the logarithm of the Coulomb matrix.
import numpy as np
plt.figure(figsize=(8, 8), dpi=150)
plt.imshow(np.log(cm_bicyclobutane), cmap='coolwarm')
plt.colorbar(label='log(magnitude)')
plt.title('Logarithm of the Coulomb Matrix for Bicyclobutane')
plt.show()
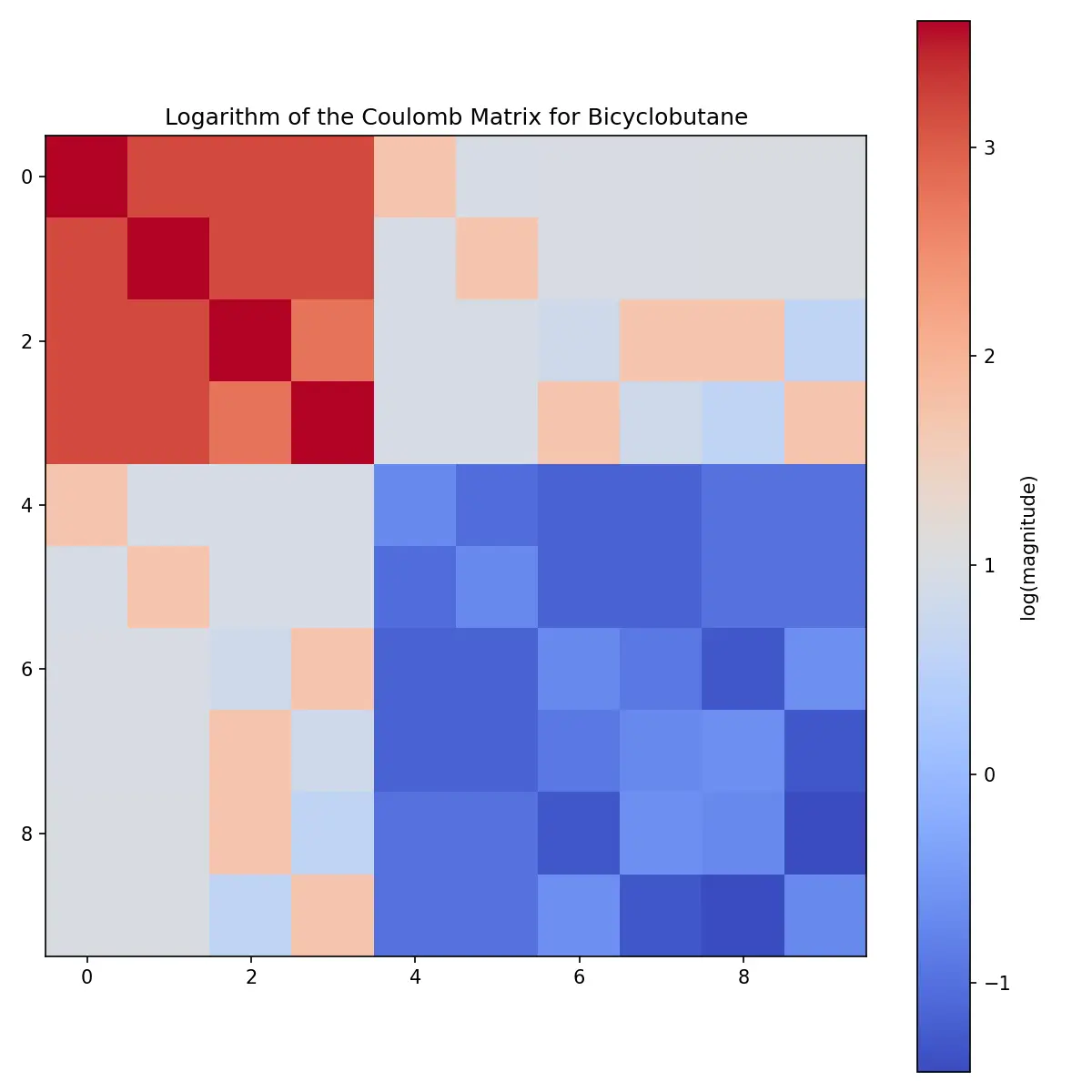
Logarithm of the Coulomb matrix of Bicyclobutane
Additionally, we can visualize the eigenvalues of the Coulomb matrix.
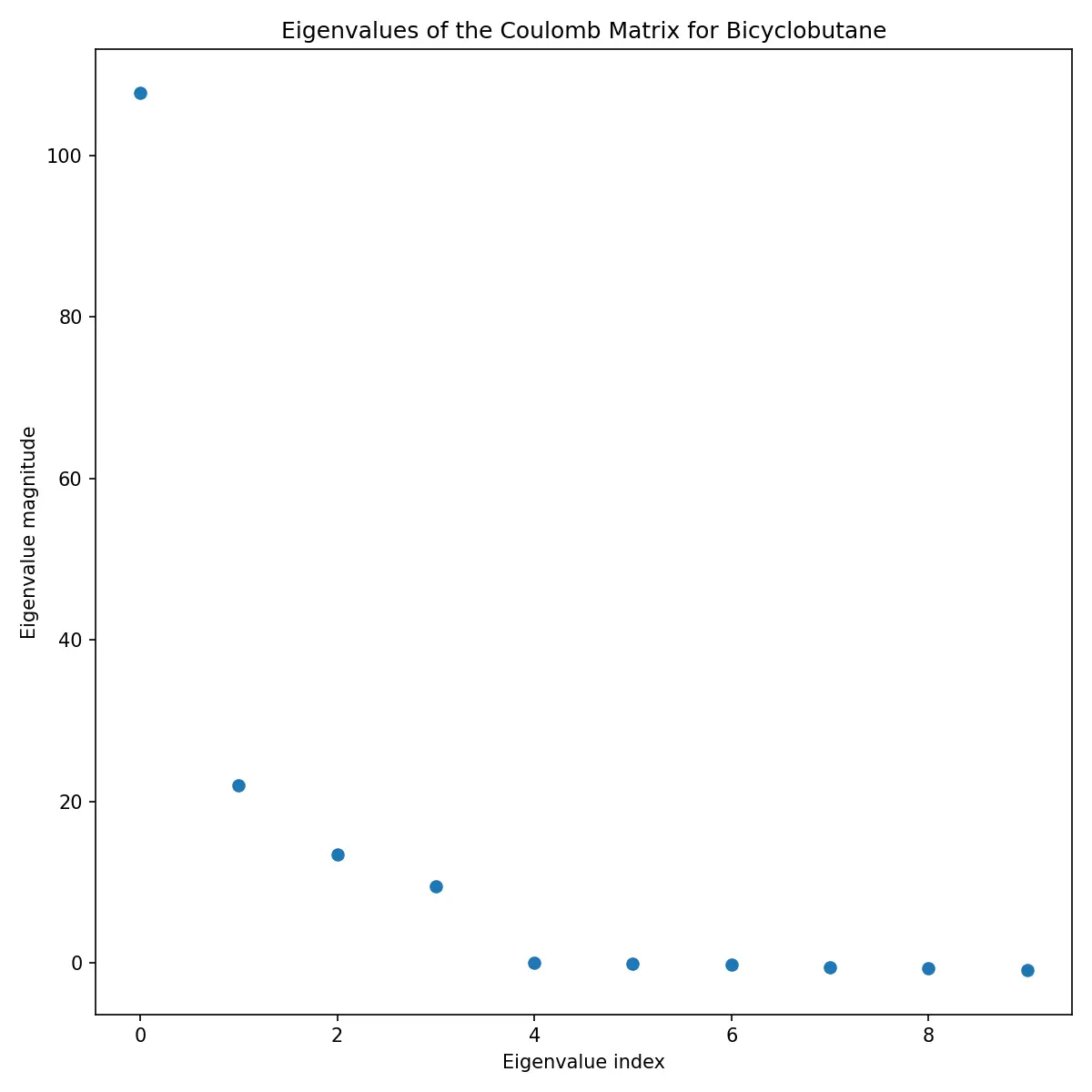
Eigenvalues of the Coulomb matrix of Bicyclobutane
Or the eigenvalues of the logarithm of the Coulomb matrix.
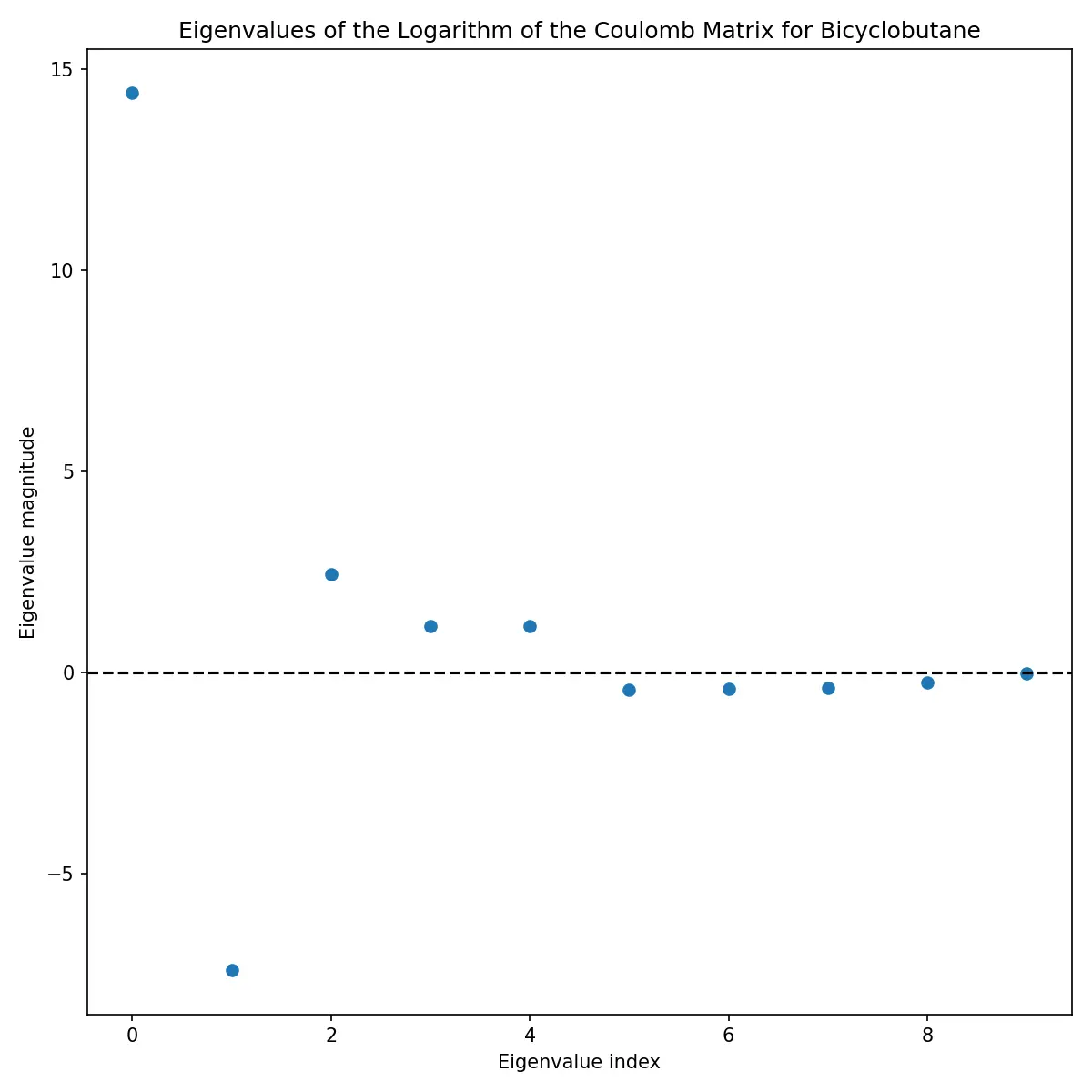
Eigenvalues of the logarithm of the Coulomb matrix of Bicyclobutane
Issues with the Coulomb Matrix
The Coulomb matrix is a very simple representation of a molecule. It’s a good introduction to the concept of molecular representations, but it has some critical limitations:
Fixed Size
The Coulomb matrix has a fixed size, which is the number of atoms in the molecule. This means that it can only represent molecules with the same number of atoms, $N$.
For molecules with less than $N$ atoms, we can pad the Coulomb matrix with zeros. This is convenient and correct, but it’s not very informative. It also prevents us from taking a logarithm of the Coulomb matrix, as we would have to deal with the zeros.
For molecules with more than $N$ atoms, we can no longer use the Coulomb matrix. This means that if you wish to use the Coulomb matrix to represent a dataset of molecules, you need to know the maximum number of atoms in the dataset in advance and pad all the Coulomb matrices to that size.
Dimensionality
The dimensionality of the Coulomb matrix is $N^2$, where $N$ is the number of atoms in the molecule. This means that the Coulomb matrix is very high-dimensional, and it can be computationally expensive to work with. Factoring in the previous point, this means that we need to pay $N_{\text{max}}^2$ for every molecule in the dataset, where $N_{\text{max}}$ is the maximum number of atoms in the dataset. That’s horribly inefficient.
One way of dealing with this is to use the eigenvalues of the Coulomb matrix, which are only $N$-dimensional. While this scales better, know that you are losing a significant amount of information by doing this. For example, distinguishing between different constitutional isomers of the same molecule becomes difficult [3]. Past studies have shown better results with the full Coulomb matrix than with the eigenvalues [5].
Permutation Invariance
One detail I’ve glossed under the rug is that the Coulomb matrix is not permutation invariant. This means that the Coulomb matrix for the same molecule can be different if the atoms are permuted.
By default, DScribe sorts rows and columns of the Coulomb matrix by their L2 norm.
This is a common way of dealing with the permutation invariance of the Coulomb matrix, but it’s not perfect
as demonstrated by [5].
Instead, one can add a bit of noise to induce likely permutations of indices based on L2 norms sorting.
This was shown to be extremely effective, especially when used to augment training data for standard
feed-forward neural networks [5].
Aperiodicity
The Coulomb matrix should never be used for periodic systems. There are alternate representations for periodic systems, such as the Ewald sum matrix or Sine matrix [6]. We’ll talk about these another time.
Conclusion
The Coulomb matrix is a simple and intuitive representation of a molecule. It’s a good starting point for understanding molecular representations, but it has some critical limitations. It’s fixed-size, high-dimensional, and not permutation invariant. Nonetheless, it’s a good starting point for understanding molecular representations and has a historical position in the field of machine learning for molecular properties [1].
If you’ve enjoyed this post or have any questions, feel free to reach out to me. If you’d like to see the Coulomb matrix in action, I’ve written a three-part series replicating the study of [3].
- Part 1: Can One Hear the Shape of a Molecule? Data Preparation and Analysis
- Part 2: Can One Hear the Shape of a Molecule? Unsupervised Learning
- Part 3: Can One Hear the Shape of a Molecule? Supervised Learning
References
- [1]: M. Rupp, A. Tkatchenko, K.-R. Müller, and O. A. von Lilienfeld, “Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning,” Physical Review Letters, 108(5), 058301 (2012). https://doi.org/10.1103/PhysRevLett.108.058301 arXiv:1109.2618
- [2] L. Himanen, M. O. J. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke, and A. S. Foster, “DScribe: Library of descriptors for machine learning in materials science,” Computer Physics Communications, 247, 106949 (2020). https://doi.org/10.1016/j.cpc.2019.106949 arXiv:1904.08875
- [3] J. Schrier, “Can one hear the shape of a molecule (from its Coulomb matrix eigenvalues)?,” Journal of Chemical Information and Modeling, 60(8), 3804-3811 (2020). https://doi.org/10.1021/acs.jcim.0c00631
- [4] A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng, and K. W. Jacobsen, “The Atomic Simulation Environment—A Python library for working with atoms,” J. Phys.: Condens. Matter, 29, 273002 (2017). https://doi.org/10.1088/1361-648X/aa680e documentation
- [5] G. Montavon, K. Hansen, S. Fazli, M. Rupp, F. Biegler, A. Ziehe, A. Tkatchenko, A. Lilienfeld, and K.-R. Müller, “Learning invariant representations of molecules for atomization energy prediction,” Advances in Neural Information Processing Systems, 25 (2012). Available online: https://proceedings.neurips.cc/paper_files/paper/2012/file/115f89503138416a242f40fb7d7f338e-Paper.pdf
- [6] F. Faber, A. Lindmaa, O. A. von Lilienfeld, and R. Armiento, “Crystal structure representations for machine learning models of formation energies,” International Journal of Quantum Chemistry, 115(16), 1094-1101 (2015). https://doi.org/10.1002/qua.24917