Introduction
If you’re new to GANs, I recommend starting with my introductory post on GANs to understand the fundamental concepts. This post dives deep into the various objective functions that power different GAN architectures and how they address specific training challenges.
TL;DR: Here’s a quick reference for the GAN variants we’ll explore:
| GAN Variant | Key Innovation | Main Benefit |
|---|---|---|
| Original GAN | Jensen-Shannon divergence | Foundation of adversarial training |
| WGAN | Earth-Mover distance | Meaningful loss, better stability |
| Improved WGAN | Gradient penalty vs. weight clipping | Eliminates weight clipping issues |
| LSGAN | Least squares loss | Better gradients, less saturation |
| RWGAN | Relaxed Wasserstein framework | Balance between WGAN variants |
| McGAN | Mean/covariance matching | Statistical feature alignment |
| GMMN | Maximum mean discrepancy | No discriminator needed |
| MMD GAN | Adversarial kernels for MMD | Improved GMMN performance |
| Cramer GAN | Cramer distance | Unbiased sample gradients |
| Fisher GAN | Chi-square distance | Training stability + efficiency |
| EBGAN | Autoencoder discriminator | Reconstruction-based losses |
| BEGAN | Boundary equilibrium | WGAN + EBGAN hybrid |
| MAGAN | Adaptive margin | Dynamic loss boundaries |
Why Objective Functions Matter
The objective function is the mathematical heart of any GAN – it defines how we measure the “distance” between our generated distribution and the real data distribution. This choice profoundly impacts:
- Training stability: Some objectives lead to more stable convergence
- Sample quality: Different losses emphasize different aspects of realism
- Mode collapse: The tendency to generate limited variety
- Computational efficiency: Some objectives are faster to compute
The original GAN uses Jensen-Shannon Divergence (JSD), but researchers have discovered many alternatives that address specific limitations. Let’s explore this evolution.
The Original GAN: Jensen-Shannon Divergence
The foundational GAN minimizes the Jensen-Shannon Divergence:
$$ \text{JSD}(P, Q) = \frac{1}{2} \text{KL}(P || M) + \frac{1}{2} \text{KL}(Q || M) $$
Where $M = \frac{1}{2}(P + Q)$ is the average distribution, and $\text{KL}$ is the Kullback-Leibler Divergence.
Strengths: Solid theoretical foundation, introduced adversarial training
Limitations: Can suffer from vanishing gradients and mode collapse
Wasserstein GAN (WGAN): A Mathematical Revolution
The Wasserstein GAN revolutionized GAN training by replacing Jensen-Shannon divergence with the Earth-Mover (Wasserstein) distance.
Understanding Earth-Mover Distance
The Wasserstein distance, also known as Earth-Mover distance, has an intuitive interpretation:
Imagine two probability distributions as piles of dirt. The Earth-Mover distance measures the minimum cost to transform one pile into the other, where cost = mass × distance moved.
Mathematically:
$$ W_p(\mu, \nu) = \left( \inf_{\gamma \in \Gamma(\mu, \nu)} \int_{M \times M} d(x, y)^p \, d\gamma(x, y) \right)^{1/p} $$
Why Earth-Mover Distance Matters
| Jensen-Shannon Divergence | Earth-Mover Distance |
|---|---|
| Can be discontinuous | Always continuous |
| May have vanishing gradients | Meaningful gradients everywhere |
| Limited convergence guarantees | Broader convergence properties |
WGAN Implementation
Since we can’t compute Wasserstein distance directly, WGAN uses the Kantorovich-Rubinstein duality:
- Train a critic function $f$ to approximate the Wasserstein distance
- Constrain the critic to be 1-Lipschitz (using weight clipping)
- Optimize the generator to minimize this distance
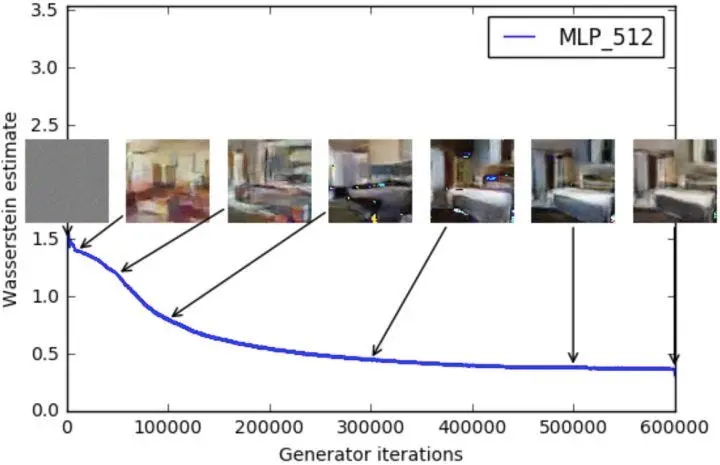
Key WGAN Benefits
Meaningful loss function: Loss correlates with sample quality
Improved stability: Less prone to mode collapse
Theoretical guarantees: Solid mathematical foundation
Better convergence: Works even when distributions don’t overlap
Improved WGAN: Solving the Weight Clipping Problem
Improved WGAN (WGAN-GP) addresses a critical flaw in the original WGAN: weight clipping.
The Problem with Weight Clipping
Original WGAN clips weights to maintain the 1-Lipschitz constraint:
# Problematic approach
for param in critic.parameters():
param.data.clamp_(-0.01, 0.01)
Issues with clipping:
- Forces critic to use extremely simple functions
- Pushes weights toward extreme values (±c)
- Can lead to poor gradient flow
- Capacity limitations hurt performance
The Gradient Penalty Solution
Instead of weight clipping, WGAN-GP adds a gradient penalty term:
$$ L = E_{\tilde{x} \sim P_g}[D(\tilde{x})] - E_{x \sim P_r}[D(x)] + \lambda E_{\hat{x}}[(||\nabla_{\hat{x}} D(\hat{x})||_2 - 1)^2] $$
Where $\hat{x}$ are points sampled uniformly along straight lines between real and generated data points.
Advantages:
- No capacity limitations
- Better gradient flow
- More stable training
- Works across different architectures
LSGAN: The Power of Least Squares
Least Squares GAN takes a different approach: replace the logarithmic loss with L2 (least squares) loss.
Motivation: Beyond Binary Classification
Traditional GANs use log loss, which focuses primarily on correct classification:
- Real sample correctly classified → minimal penalty
- Fake sample correctly classified → minimal penalty
- Distance from decision boundary ignored
L2 Loss: Distance Matters
LSGAN uses L2 loss, which penalizes proportionally to distance:
$$ \min_D V_{LSGAN}(D) = \frac{1}{2}E_{x \sim p_{data}(x)}[(D(x) - b)^2] + \frac{1}{2}E_{z \sim p_z(z)}[(D(G(z)) - a)^2] $$
$$ \min_G V_{LSGAN}(G) = \frac{1}{2}E_{z \sim p_z(z)}[(D(G(z)) - c)^2] $$
Where typically: $a = 0$ (fake label), $b = c = 1$ (real label)
Benefits of L2 Loss
| Log Loss | L2 Loss |
|---|---|
| Binary focus | Distance-aware |
| Can saturate | Informative gradients |
| Sharp decision boundary | Smooth decision regions |

Key insight: LSGAN minimizes the Pearson χ² divergence, providing smoother optimization landscape than JSD.
Relaxed Wasserstein GAN (RWGAN)
Relaxed WGAN bridges the gap between WGAN and WGAN-GP, proposing a general framework for designing GAN objectives.
Key Innovations
Asymmetric weight clamping: Instead of symmetric clamping (original WGAN) or gradient penalties (WGAN-GP), RWGAN uses an asymmetric approach that provides better balance.
Relaxed Wasserstein divergences: A generalized framework that extends the Wasserstein distance, enabling systematic design of new GAN variants while maintaining theoretical guarantees.
Benefits
- Better convergence properties than standard WGAN
- Framework for designing new loss functions and GAN architectures
- Competitive performance with state-of-the-art methods
Key insight: RWGAN parameterized with KL divergence shows excellent performance while maintaining the theoretical foundations that make Wasserstein GANs attractive.
Statistical Distance Approaches
Several GAN variants focus on minimizing specific statistical distances between distributions.
McGAN: Mean and Covariance Matching
McGAN belongs to the Integral Probability Metric (IPM) family, using statistical moments as the distance measure.
Approach: Match first and second-order statistics:
- Mean matching: Align distribution centers
- Covariance matching: Align distribution shapes
Limitation: Relies on weight clipping like original WGAN.
GMMN: Maximum Mean Discrepancy
Generative Moment Matching Networks eliminates the discriminator entirely, directly minimizing Maximum Mean Discrepancy (MMD).
MMD Intuition: Compare distributions by their means in a high-dimensional feature space:
$$ \text{MMD}^2(X, Y) = ||E[\phi(x)] - E[\phi(y)]||^2 $$
Benefits:
- Simple, discriminator-free training
- Theoretical guarantees
- Can incorporate autoencoders for better MMD estimation
Drawbacks:
- Computationally expensive
- Often weaker empirical results
MMD GAN: Learning Better Kernels
MMD GAN improves GMMN by learning optimal kernels adversarially rather than using fixed Gaussian kernels.
Innovation: Combine GAN adversarial training with MMD objective for the best of both worlds.
Different Distance Metrics
Cramer GAN: Addressing Sample Bias
Cramer GAN identifies a critical issue with WGAN: biased sample gradients.
The Problem: WGAN’s Wasserstein distance lacks three important properties:
- Sum invariance (satisfied)
- Scale sensitivity (satisfied)
- Unbiased sample gradients (not satisfied)
The Solution: Use the Cramer distance, which satisfies all three properties:
$$ d_C^2(\mu, \nu) = \int ||E_{X \sim \mu}[X - x] - E_{Y \sim \nu}[Y - x]||^2 d\pi(x) $$
Benefit: More reliable gradients lead to better training dynamics.
Fisher GAN: Chi-Square Distance
Fisher GAN uses a data-dependent constraint on the critic’s second-order moments (variance).
Key Innovation: The constraint naturally bounds the critic without manual techniques:
- No weight clipping needed
- No gradient penalties required
- Constraint emerges from the objective itself
Distance: Approximates the Chi-square distance as critic capacity increases:
$$ \chi^2(P, Q) = \int \frac{(P(x) - Q(x))^2}{Q(x)} dx $$
The Fisher GAN essentially measures the Mahalanobis distance, which accounts for correlated variables relative to the distribution’s centroid. This ensures the generator and critic remain bounded, and as the critic’s capacity increases, it estimates the Chi-square distance.
Benefits:
- Efficient computation
- Training stability
- Unconstrained critic capacity
RWGAN: Relaxed Framework
Relaxed WGAN proposes a general framework for designing GAN objectives.
Innovation: Asymmetric weight clamping instead of:
- Symmetric clamping (original WGAN)
- Gradient penalties (WGAN-GP)
Framework: Introduces “Relaxed Wasserstein divergences” that generalize the Wasserstein distance, enabling systematic design of new GAN variants.
Result: Better convergence than WGAN while maintaining theoretical guarantees.
Beyond Traditional GANs: Alternative Approaches
The following variants explore fundamentally different architectures and training paradigms.
EBGAN: Energy-Based Discrimination
Energy-Based GAN replaces the discriminator with an autoencoder.
Key insight: Use reconstruction error as the discrimination signal:
- Good data → Low reconstruction error
- Poor data → High reconstruction error
Architecture:
- Train autoencoder on real data
- Generator creates samples
- Poor generated samples have high reconstruction loss
- This loss drives generator improvement
Benefits:
- Fast and stable training
- Robust to hyperparameter changes
- No need to balance discriminator/generator
BEGAN: Boundary Equilibrium
BEGAN combines EBGAN’s autoencoder approach with WGAN-style loss functions.
Innovation: Dynamic equilibrium parameter $k_t$ that balances:
- Real data reconstruction quality
- Generated data reconstruction quality
Equilibrium equation:
$$ L_D = L(x) - k_t L(G(z)) $$
$$ k_{t+1} = k_t + \lambda(\gamma L(x) - L(G(z))) $$
MAGAN: Adaptive Margins
MAGAN improves EBGAN by making the margin in the hinge loss adaptive over time.
Concept: Start with a large margin, gradually reduce it as training progresses:
- Early training: Focus on major differences
- Later training: Fine-tune subtle details
Result: Better sample quality and training stability.
Summary: The Evolution of GAN Objectives
The evolution of GAN objective functions reflects the field’s progression toward more stable and theoretically grounded training procedures. Each variant addresses specific limitations in earlier approaches.
Complete Reference Table
| GAN Variant | Key Innovation | Main Benefit | Limitation |
|---|---|---|---|
| Original GAN | Jensen-Shannon divergence | Foundation of adversarial training | Vanishing gradients, mode collapse |
| WGAN | Earth-Mover distance | Meaningful loss, better stability | Weight clipping issues |
| WGAN-GP | Gradient penalty | Solves weight clipping problems | Additional hyperparameter tuning |
| LSGAN | Least squares loss | Better gradients, less saturation | May converge to non-optimal points |
| RWGAN | Relaxed Wasserstein framework | General framework for new designs | Complex theoretical setup |
| McGAN | Mean/covariance matching | Simple statistical alignment | Limited by weight clipping |
| GMMN | Maximum mean discrepancy | No discriminator needed | Computationally expensive |
| MMD GAN | Adversarial kernels for MMD | Improved GMMN performance | Still computationally heavy |
| Cramer GAN | Cramer distance | Unbiased sample gradients | Complex implementation |
| Fisher GAN | Chi-square distance | Self-constraining critic | Limited empirical validation |
| EBGAN | Autoencoder discriminator | Fast, stable training | Requires careful regularization |
| BEGAN | Boundary equilibrium | Dynamic training balance | Additional equilibrium parameter |
| MAGAN | Adaptive margin | Progressive refinement | Margin scheduling complexity |
Key Observations
- Distance metrics matter: The choice of distance function fundamentally affects training dynamics and convergence properties.
- Constraint mechanisms are crucial: How we constrain the discriminator/critic determines training stability.
- Theoretical foundations drive practical improvements: Methods with solid mathematical foundations tend to perform better in practice.
- Trade-offs are inevitable: Different objectives optimize for different aspects of generation quality and training stability.
Practical Recommendations
For practitioners, the choice depends on specific requirements:
- WGAN-GP: Best balance of stability and performance for most applications
- LSGAN: Simpler implementation with good empirical results
- EBGAN: Fast experimentation and prototyping
- Original GAN: Educational purposes and understanding fundamentals
The field continues evolving, with modern approaches like StyleGAN, BigGAN, and diffusion models building on these foundational insights about objective functions and training dynamics.
The choice of GAN objective function depends on your specific requirements for generation quality, training stability, and computational constraints. Understanding these different approaches provides the foundation for selecting the right method for your application. For those new to GANs, I recommend starting with the fundamental concepts before experimenting with these objective functions.
