Introduction - Can One Hear the Shape of a Molecule?
Recently, I was reading the paper “Can One Hear the Shape of a Molecule (from its Coulomb Matrix Eigenvalues)?” while thinking about Coulomb Matrices.
The paper’s title is a play on the famous question “Can One Hear the Shape of a Drum?” by Mark Kac. The question asks whether the shape of a drum can be determined by the sound it makes, using the eigenvalues of the Laplacian operator on the drum’s surface as a signature. In contrast, the molecule paper asks whether the shape of a molecule can be determined by the eigenvalues of its Coulomb matrix analogously to the drum question.
The paper isn’t saying anything fundamental about alkanes, but rather it’s using them as a test case to explore the question of whether the Coloumb matrix eigenvalues are sufficient for identifying molecular shape. Aligned with my own skill set, they use machine learning (both supervised and unsupervised) to measure the ease of classifying alkanes based on their Coulomb matrix eigenvalues.
I found the paper interesting and straightforward, and I thought it would be fun to try to replicate their results. As I don’t have access to things like Mathematica, I’ll discuss alternate methods for things like generating extensive lists of structural isomers that I found to be sufficient for my own purposes.
In order to make these posts more digestible, I’ll break the replication into a series of posts:
- This post will focus on isomer and conformer generation, Coulomb matrix calculation, and eigenvalue calculation. We’ll plot aspects of the generated data to compare directly with the paper to validate our generation process.
- The next post will focus on unsupervised learning, where we’ll use clustering to see if the Coulomb matrix eigenvalues can naturally separate the isomers. We’ll leverage metrics like the silhouette score to measure the quality of the clustering.
- The final post will focus on supervised learning, where we’ll use the Coulomb matrix eigenvalues as features to train a classifier to distinguish between the isomers. We’ll use metrics like accuracy, precision, recall, and F1 score to measure the quality of the classifier.
Along the way, we’ll also slightly experiment with the idea of using log-transformed Coloumb matrices. As we saw in the Coulomb matrix post, the Coulomb matrix has a wider distribution of magnitude across its eigenspectra when we first transform the Coloumb matrix with a log transformation.
Alkanes - A Test Case for Molecular Shape
Alkanes are a class of hydrocarbons that consist of only carbon and hydrogen atoms, with no double or triple bonds. Specifically, we adhere to the IUPAC definition of alkanes:
acyclic branched or unbranched hydrocarbons having the general formula $C_{n}H_{2n+2}$, and therefore consisting entirely of hydrogen atoms and saturated carbon atoms
They are the simplest class of organic compounds, and they are the basis for many other classes of organic compounds. This makes them an excellent test bed for exploring the question of whether the shape of a molecule can be determined by its Coulomb matrix eigenvalues.
Beyond alkanes generally, we’re interested in the constitutional isomers of alkanes. A constitutional isomer is a molecule that has the same molecular formula as another molecule, but with a different arrangement of atoms. In the case of alkanes, this means we’re interested in all the different ways one can arrange $n$ carbon atoms and $2n+2$ hydrogen atoms, whether linear or branched.
For small alkanes ($n \le 3$), there are no constitutional isomers, but for $n=4$, there are two constitutional isomers: butane and isobutane.
Butane as a ball-and-stick model. Butane is a linear alkane, sometimes called n-butane. (source)
Isobutane as a ball-and-stick model. Isobutane is a branched alkane, sometimes called 2-methylpropane. (source)
Therefore, when we start our classification questions, we’ll begin with $n=4$ (skipping methane ($n=1$), ethane ($n=2$), and propane ($n=3$) as they have no constitutional isomers), and we’ll go up to $n=11$ (undecane).
In the supplemental information of the original paper, they provide a table of the number of constitutional isomers and stereoisomers for alkanes up to $n=11$:
| Name | $n$ | Constitutional Isomers | Stereoisomers |
|---|---|---|---|
| Methane | 1 | 1 | 0 |
| Ethane | 2 | 1 | 0 |
| Propane | 3 | 1 | 0 |
| Butane | 4 | 2 | 0 |
| Pentane | 5 | 3 | 0 |
| Hexane | 6 | 5 | 0 |
| Heptane | 7 | 9 | 2 |
| Octane | 8 | 18 | 5 |
| Nonane | 9 | 35 | 15 |
| Decane | 10 | 75 | 40 |
| Undecane | 11 | 159 | 104 |
From this table, we can see that the number of constitutional isomers grows rapidly with $n$.
- Note: The paper focuses on constitutional isomers, but it’s worth noting that the number of stereoisomers also grows rapidly with $n$. The paper readily acknowledges that it’s not storing information about stereoisomers, instead viewing a constitutional isomer as a racemic mixture of all its stereoisomers.
In our task of classifying constitutional isomers, we restrict to a particular value of $n$ and generate a list of constitutional isomers. These constitutional isomers represent the different classes in our classification task.
- For $n=4$, we have two classes: butane and isobutane.
- For $n=11$, we have 159 classes. An extremely difficult classification task!
For each class, we need to generate samples of the isomer’s 3D structure, calculate the Coulomb matrix, and then calculate the eigenvalues of the Coulomb matrix. This forms the basis of our feature set for classification, supervised or unsupervised.
In this post, we focus on generating the isomers and their 3D structures, calculating the Coulomb matrix, and calculating the eigenvalues of the Coulomb matrix. So, let’s begin with writing some code to generate the constitutional isomers for $n=1$ and $n=11$.
Generating Alkane Isomers - A Combinatorial Problem
How do we generate the constitutional isomers for alkanes? In general, this is a combinatorial problem and can be quite difficult. Most of the time, we necessarily make simplifying assumptions to make the problem more tractable. Beyond that, parallelization is key to making the problem feasible for larger $n$. In the original paper, the author relies on mathematica (which I don’t have access to) to generate the conformers, and I think it’s important to discuss alternate methods for generating conformers that are accessible to everyone.
My solution was to use MAYGEN (MAYGEN GitHub). I really like it because it’s open source, and it’s a command line tool that can be run on any computer. It uses Java under the hood and I found it to be quite fast and efficient.
As an example, to generate the isomers for $n=4$, I ran the following command:
java -jar MAYGEN-1.8.jar -v -m -f C4H10 -smi -o butane_conformers.smi
-vis for verbose output-mis to enable multithreading-f C4H10specifies the molecular formula-smispecifies the output format as SMILES-o butane_conformers.smispecifies the output file
You should see console output similar to the following:
MAYGEN is generating isomers of C4H10...
The number of structures is: 2
Time: .116 seconds
If you inspect the output file butane_conformers.smi, you’ll see the following:
CCCC
CC(C)C
pretty much as expected.
To further automate the generation of isomers for alkanes up to $n=11$, I wrote a simple Python code to generate the isomers using MAYGEN:
os.makedirs('isomers', exist_ok=True)
for n in range(1, 12):
# check if the file already exists
if os.path.exists(f'isomers/C{n}H{2*n+2}.smi'):
continue
cmd_str = f'java -jar MAYGEN-1.8.jar -v -m -smi -f C{n}H{2*n+2} -o isomers/'
os.system(cmd_str)
If you want to get canonical names for the isomers, you can do something like the following to query the PubChem database:
import requests
def get_iupac_name(smiles):
url = f"https://pubchem.ncbi.nlm.nih.gov/rest/pug/compound/smiles/{smiles}/property/IUPACName/JSON"
response = requests.get(url)
if response.status_code == 200:
data = response.json()
return data['PropertyTable']['Properties'][0]['IUPACName']
else:
return "Error: Could not retrieve data"
# Example usage
n = 7
with open(f'isomers/C{n}H{2*n + 2}.smi') as f:
for line in f:
smiles = line.strip()
print(smiles, get_iupac_name(smiles))
which should, for heptane, print something like:
CCCCCCC heptane
CCC(CC)CC 3-ethylpentane
CC(C)CC(C)C 2,4-dimethylpentane
CC(C)C(C)(C)C 2,2,3-trimethylbutane
CCC(C)(C)CC 3,3-dimethylpentane
CCC(C)C(C)C 2,3-dimethylpentane
CCCC(C)CC 3-methylhexane
CCCC(C)(C)C 2,2-dimethylpentane
CCCCC(C)C 2-methylhexane
Generating Conformers (3D Structures) - A Computational Chemistry Problem
In order to create training data for our machine learning models, we need to generate 3D structures for each isomer. The paper uses RDKit to generate the 3D structures, relying on the ETKDG method for conformer generation. According to past studies on conformer generation, ETKDG is free and still competitive with commercial alternatives.
We write a simple Python function to achieve this like so:
After generating the 3D structures, we’ll use DScribe to calculate the Coulomb matrix, which is invariant to translation and rotation of the molecule.
Before doing so, let’s first write a helper function to transform RDKit molecules into ase.Atoms objects, the Atomic Simulation Environment object that DScribe can work with.
With that, we can now compute the Coulomb matrix for each conformer using DScribe and compute the eigenvalues with numpy, allowing for an optional log transformation of the Coloumb matrix prior to eigenvalue calculation.
Using these helper functions, we can sample a batch of conformers, calculate their Coulomb matrices, and calculate the eigenvalues of the Coulomb matrices quite directly:
def gen_n_spectra(
n: int,
smiles_str: str,
log: bool = False
) -> np.ndarray:
"""Generate n Coulomb matrix eigenvalue spectra for a molecule.
Args:
n: Number of spectra to generate.
smiles_str: SMILES string of the molecule.
log: Whether to log transform the Coulomb matrix prior to calculating the eigenvalues.
Returns:
Eigenvalue spectra.
"""
spectra = []
for _ in tqdm(range(n)):
# Convert SMILES string to RDKit mol object
mol = smiles_str_to_rdkit_mol(smiles_str)
# Convert RDKit mol object to ASE Atoms object
atoms = rdkit_mol_to_ase_atoms(mol)
# Generate Coulomb matrix eigenvalue spectra
spectra.append(ase_atoms_to_coloumb_matrix_eigenvalues(atoms, log=log))
# Convert to numpy array
spectra = np.array(spectra)
return spectra
Validating the Generation Process
In the remainder of this post, I’d like to go through the Figures of the original paper and compare them to similar figures generated from our own code. This will help us validate our generation process and ensure that we’re on the right track for the next steps of unsupervised and supervised learning.
To start, we’ll generate the data for this section using the following code:
os.makedirs('spectra', exist_ok=True)
n_confs = 1000
for n in range(1, 12):
print(f'Generating spectra for C{n}H{2*n + 2}')
with open(f'isomers/C{n}H{2*n + 2}.smi') as f:
lines = f.readlines()
print(f'\tNumber of SMILES strings: {len(lines)}')
for i, line in enumerate(tqdm(lines)):
print(f'\t\t{i + 1}/{len(lines)} - {line.strip()}')
if not line.strip():
continue
if os.path.exists(f'spectra/C{n}H{2*n + 2}_{i}.npy'):
continue
smiles = line.strip()
spectra = gen_n_spectra(n=n_confs, smiles_str=smiles, log=False)
np.save(f'spectra/C{n}H{2*n + 2}_{i:03d}.npy', spectra)
As this will take a non-trivial amount of time, be sure to cache it to disk so you don’t have to re-run it!
Then, we can reload the data into a structured format:
import re
from glob import glob
spectra = {}
for n in range(1, 12):
if n not in spectra:
spectra[n] = {}
for i, f in enumerate(glob(f'spectra/C{n}H{2*n + 2}_*.npy')):
j = int(re.search(rf'C{n}H{2*n + 2}_(\d+).npy', f).group(1))
spectra[n][j] = np.load(f)
print(f'Loaded {len(spectra[n])}k spectra for C{n}H{2*n + 2}')
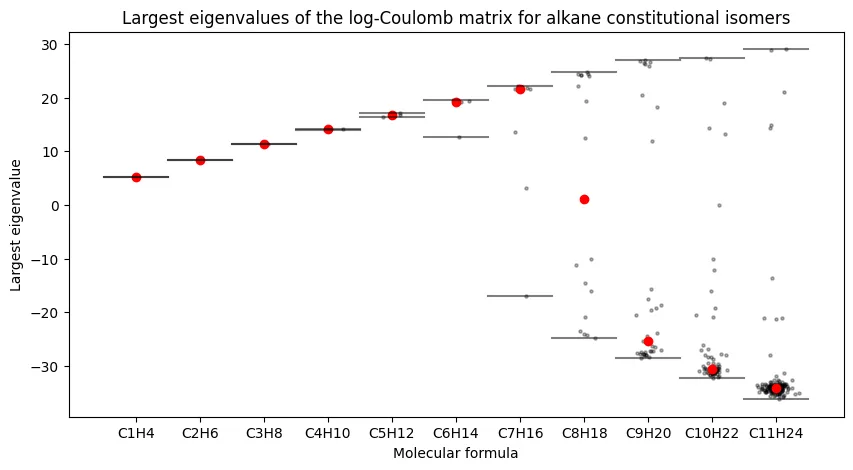
Figure 1 - Largest Eigenvalues of the Coulomb Matrix for Alkane Constitutional Isomers
The first figure of the paper shows the box plots of the largest Eigenvalues of the Coulomb matrix for all alkane constitutional isomers up to $n=11$. Each molecular formula makes up a box plot with individual points for each isomer. This figure is used to argue that the Coulomb matrix eigenvalues are not sufficient for distinguishing between chemical formulas, at least when restricting to the largest eigenvalue.
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for n in range(1, 12):
eigenvalues = np.array([spectra[n][i][:, 0].mean() for i in spectra[n]])
# add black dots to boxplot, but not dirextly to the center line
jitter = np.random.normal(0, 0.1, size=len(eigenvalues))
ax.scatter(np.full(len(eigenvalues), n) + jitter, eigenvalues, color='black', s=1, alpha=0.3)
# Plot median
ax.scatter([n], [np.median(eigenvalues)], color='red', alpha=0.5)
# Plot range
ax.plot([n - 0.5, n + 0.5], [np.min(eigenvalues), np.min(eigenvalues)], 'k-', alpha=0.5) # Draw a line for the range
ax.plot([n - 0.5, n + 0.5], [np.max(eigenvalues), np.max(eigenvalues)], 'k-', alpha=0.5) # Draw a line for the range
ax.set_xlabel('Molecular formula')
ax.set_ylabel('Largest eigenvalue')
ax.set_xticks(range(1, 12))
ax.set_xticklabels([f'C{n}H{2*n + 2}' for n in range(1, 12)])
ax.set_title('Largest eigenvalues of the Coulomb matrix for alkane constitutional isomers')
plt.savefig('alkane_coulomb_matrix_largest_eigenvalues.webp', bbox_inches='tight')
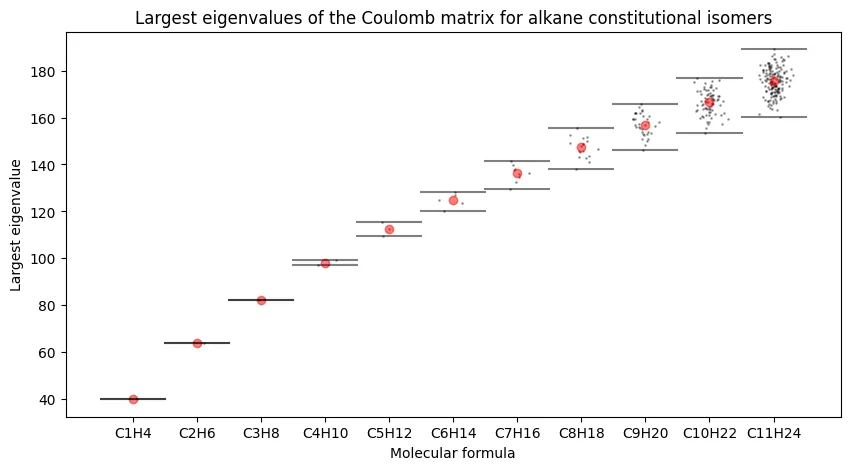
Largest eigenvalues of the Coulomb matrix for alkane constitutional isomers.
Barring stylistic differences, our plot looks quite similar to the original paper’s Figure 1. We see a sub-linear growth in the largest eigenvalue with the number of carbon atoms in the molecule, and we see that the largest eigenvalue is not likely to be sufficient for distinguishing between constitutional isomers, especially for larger $n$.
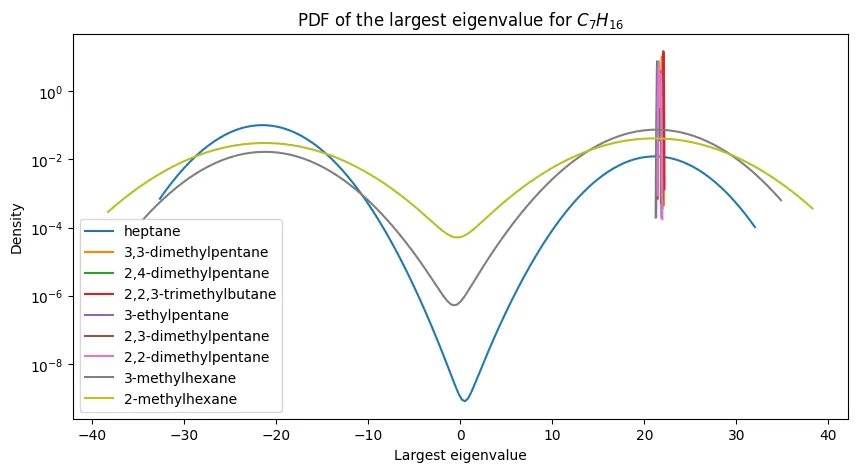
Figure 2 - Maximum Eigenvalue PDFs for $C_7H_{16}$ and Its Constitutional Isomers
The second figure of the paper shows PDFs of the largest eigenvalue for $C_7H_{16}$ (heptane) and its constitutional isomers. The paper highlights how:
- $n$-heptane conformers have the smallest maximum eigenvalue
- $2,2,3$-trimethylbutane conformers have the largest maximum eigenvalue
- all of the other seven conformers have maximum eigenvalues that are intermediate between these two extremes and are not easily distinguishable from one another
In this way, evidence is provided that the Coulomb matrix maximum eigenvalue is not sufficient for distinguishing between constitutional isomers.
for n_sel in range(4, 8):
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
smiles = []
with open(f'isomers/C{n_sel}H{2*n_sel + 2}.smi') as f:
for line in f:
smiles.append(line.strip())
for i in range(len(spectra[n_sel])):
eigenvalues = spectra[n_sel][i][:, 0]
# kde plot with the following params
# - Gaussian kernel
# - bandwidth with Silverman's rule of thumb
ax = sns.kdeplot(eigenvalues, bw_method='silverman', label=get_iupac_name(smiles[i]))
ax.set_xlabel('Largest eigenvalue')
ax.set_ylabel('Density')
ax.set_title('PDF of the largest eigenvalue for $C_' + str(n_sel) + 'H_{' + str(2*n_sel + 2) + '}$')
ax.legend()
plt.savefig(f'pdf_largest_eigenvalue_C{n_sel}H{2*n_sel + 2}.webp', bbox_inches='tight')
plt.close()
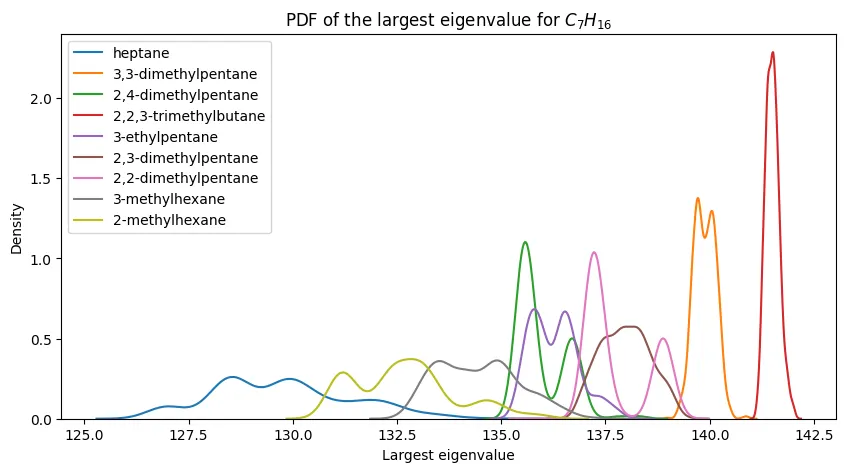
PDFs of the largest eigenvalue for $C_7H_{16}$ and its constitutional isomers.
We annotate our plot with the IUPAC names of the isomers, and we see that the PDFs are quite similar to the original paper’s Figure 2.
For the interested, you can also see the plots I generated for $n \in {4, 5, 6}$:
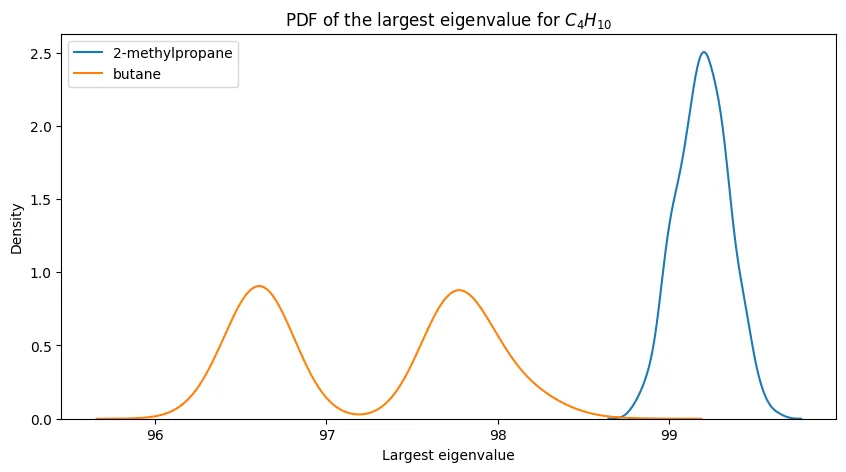
PDFs of the largest eigenvalue for $C_4H_{10}$ and its constitutional isomers.
For $n=4$, we see that the PDFs are quite distinct from one another, suggesting that the largest eigenvalue is sufficient for distinguishing between butane and isobutane. We’ll see this further confirmed next.
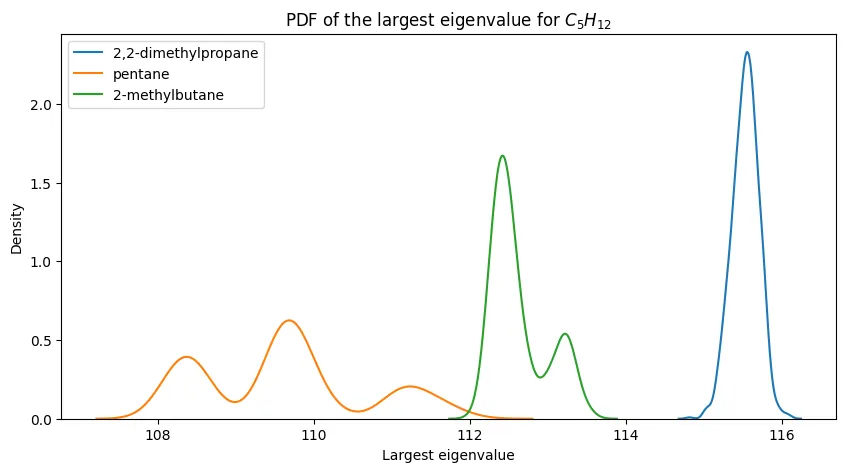
PDFs of the largest eigenvalue for $C_5H_{12}$ and its constitutional isomers.
Similar to $n=4$, we see fairly decent separation between the PDFs for pentane and its constitutional isomers, suggesting that the largest eigenvalue is sufficient for distinguishing between these isomers.
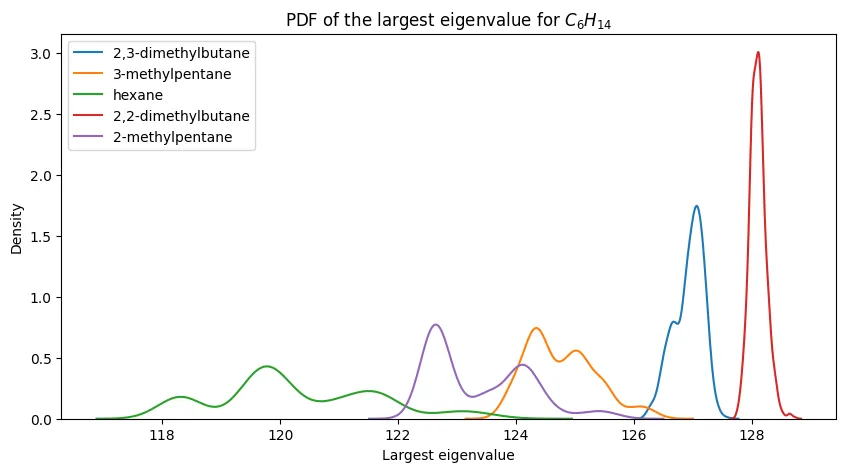
PDFs of the largest eigenvalue for $C_6H_{14}$ and its constitutional isomers.
The case of hexane is a bit more ambiguous, but we still see some separation between the PDFs for hexane and its constitutional isomers. However, two isomers (2-mehtylpentane and 3-methylpentane) have PDFs that are quite similar to one another.
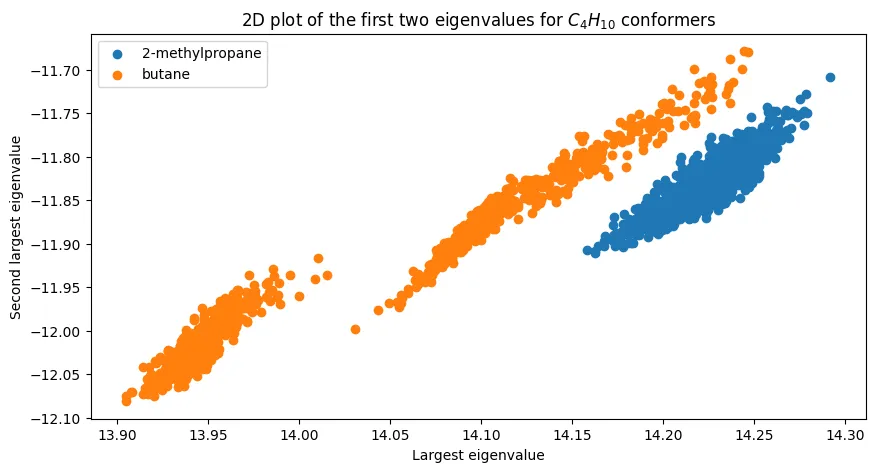
Figure 3 - 2D Space of Coulomb Matrix Eigenvalues for $C_4H_{10}$ (Butane and Isobutane)
What if we expand the scope? Look at more than just the largest eigenvalue? Figure 3 of the paper plots the two isomers of $C_4H_{10}$ (butane and isobutane) in 2D space, using the first two eigenvalues of the Coulomb matrix. This demonstrates a clear linear separation between the two isomers, suggesting that the Coulomb matrix eigenvalues are sufficient for distinguishing between these two isomers.
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
n_sel = 4
smiles = []
with open(f'isomers/C{n_sel}H{2*n_sel + 2}.smi') as f:
for line in f:
smiles.append(line.strip())
for i in range(len(spectra[n_sel])):
eigenvalues = spectra[n_sel][i][:, :2]
ax.scatter(eigenvalues[:, 0], eigenvalues[:, 1], label=get_iupac_name(smiles[i]))
ax.set_xlabel('Largest eigenvalue')
ax.set_ylabel('Second largest eigenvalue')
ax.set_title('2D plot of the first two eigenvalues for $C_4H_{10}$ conformers')
ax.legend()
plt.savefig(f'2d_largest_eigenvalue_C{n_sel}H{2*n_sel + 2}.webp', bbox_inches='tight')
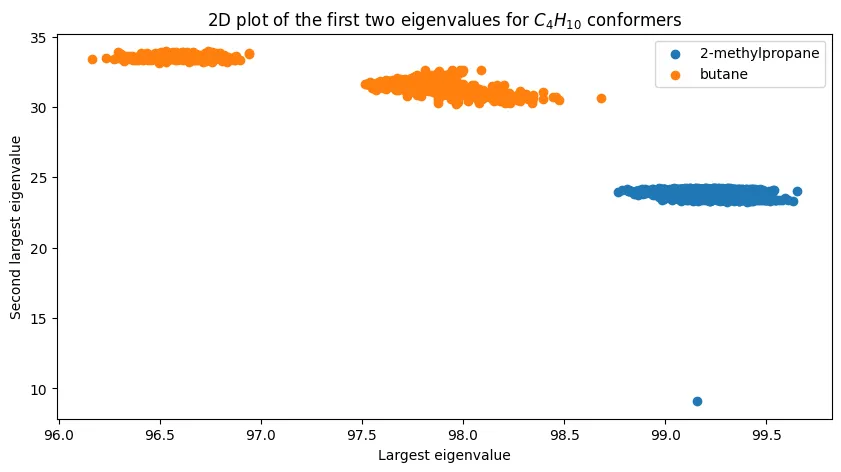
2D space of Coulomb matrix eigenvalues for $C_4H_{10}$ (butane and isobutane).
For the most part, we observe a similar plot to the original paper’s Figure 3. However, I do think we have one conformer in the lower right that seems noisy/suspicious. This could be a result of the conformer generation process, and it’s something we should consider discarding.
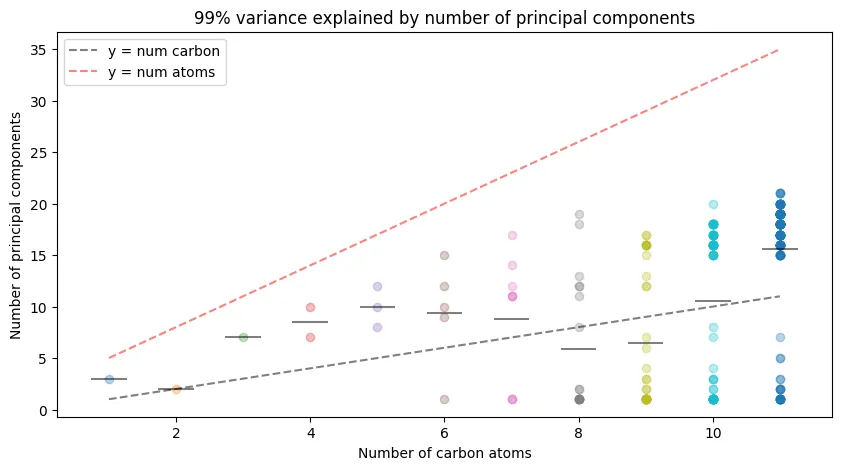
Figure 4 - Number of Principal Components Required for 99% Variance in Coulomb Matrix Eigenvalues
But is this always the case for all constitutional isomers? Definitely not! The author presents Figure 4 as a plot of the number of principal components required to describe at least 99% of the variance in the Coulomb matrix eigenvalues for each alkane constitutional isomer. This figure shows that the number of principal components required grows sub-linearly with the number of carbon atoms in the molecule, suggesting that the Coulomb matrix eigenvalues are not sufficient for distinguishing between constitutional isomers.
from sklearn.decomposition import PCA
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
n_components = {}
for n in range(1, 12):
n_components[n] = []
for i in range(len(spectra[n])):
eigenvalues = spectra[n][i]
# PCA
pca = PCA(n_components=0.99, svd_solver='full', whiten=False, random_state=42)
pca.fit(eigenvalues)
n_components[n].append(pca.n_components_)
ax.scatter([n] * len(n_components[n]), n_components[n], alpha=0.3)
ax.plot([n - 0.25, n + 0.25], [np.mean(n_components[n]), np.mean(n_components[n])], 'k-', alpha=0.5) # Draw a line for the mean
ax.plot([1, 11], [1, 11], 'k--', alpha=0.5, label='y = num carbon')
ax.plot([1, 11], [5, 35], 'r--', alpha=0.5, label='y = num atoms')
ax.set_xlabel('Number of carbon atoms')
ax.set_ylabel('Number of principal components')
ax.set_title('99% variance explained by number of principal components')
plt.legend()
plt.savefig('99_variance_explained.webp', bbox_inches='tight')
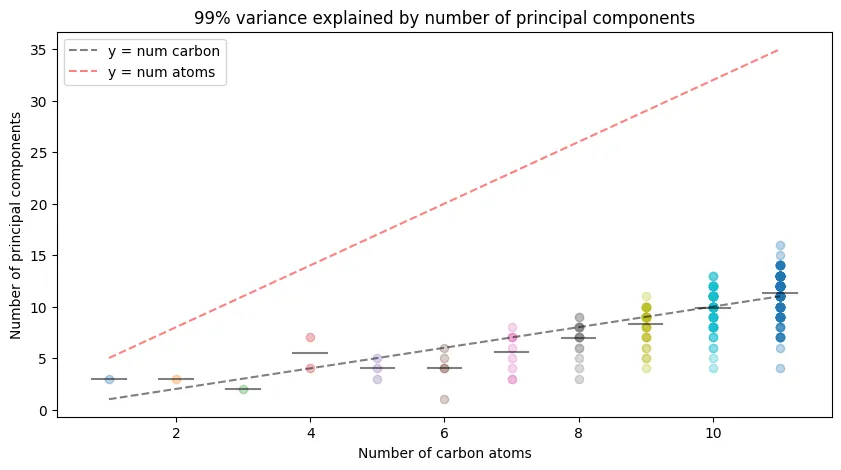
99% variance explained by number of principal components.
While I think my plot looks a bit different from the original paper’s Figure 4, I think the general trend is the same in that:
- For molecules with $N$ degrees of freedom, where $N=3n+2$ for $n$ carbon atoms, we need far less than $N$ principal components to explain 99% of the variance in the Coulomb matrix eigenvalues.
- The number of principal components required grows seemingly linearly in the number of carbon atoms in the molecule, but it’s not clear if this is a general trend.
This means the representations are highly correlated, and we can likely reduce the dimensionality of the Coulomb matrix eigenvalues without losing much information.
Experimenting with Log-Transformed Coulomb Matrices
I want to repeat the same plot generation process, but this time with log-transformed Coulomb matrices. As we saw in the Coulomb matrix post, the Coulomb matrix has a wider distribution of magnitude across its eigenspectra when we first transform the Coloumb matrix with a log transformation. Instead of down-sampling the hydrogen atoms and up-sampling heavy atoms, taking the log-transformation of the Coulomb matrix has an opposite effect: it expands the range of hydrogen atoms, as magnitudes in $[0, 1]$ are expanded to $[-\infty, 0]$.
What does that do to the eigenvalue spectra?
Let’s find out!
os.makedirs('spectra', exist_ok=True)
n_confs = 1000
for n in range(1, 12):
print(f'Generating spectra for C{n}H{2*n + 2}')
with open(f'isomers/C{n}H{2*n + 2}.smi') as f:
lines = f.readlines()
print(f'\tNumber of SMILES strings: {len(lines)}')
for i, line in enumerate(tqdm(lines)):
print(f'\t\t{i + 1}/{len(lines)} - {line.strip()}')
if not line.strip():
continue
if os.path.exists(f'spectra/log-C{n}H{2*n + 2}_{i}.npy'):
continue
smiles = line.strip()
spectra = gen_n_spectra(n=n_confs, smiles_str=smiles, log=True)
np.save(f'spectra/log-C{n}H{2*n + 2}_{i:03d}.npy', spectra)
and then:
log_spectra = {}
for n in range(1, 12):
if n not in log_spectra:
log_spectra[n] = {}
for i, f in enumerate(glob(f'spectra/log-C{n}H{2*n + 2}_*.npy')):
j = int(re.search(rf'log-C{n}H{2*n + 2}_(\d+).npy', f).group(1))
log_spectra[n][j] = np.load(f)
print(f'Loaded {len(log_spectra[n])}k spectra for C{n}H{2*n + 2}')
Figure 1 Redux - Largest Eigenvalues of the Log-Transformed Coulomb Matrix for Alkane Constitutional Isomers
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for n in range(1, 12):
eigenvalues = np.array([log_spectra[n][i][:, 0].mean() for i in log_spectra[n]])
# add black dots to boxplot, but not dirextly to the center line
jitter = np.random.normal(0, 0.1, size=len(eigenvalues))
ax.scatter(np.full(len(eigenvalues), n) + jitter, eigenvalues, color='black', s=5, alpha=0.3)
# Plot median
ax.scatter([n], [np.median(eigenvalues)], color='red')
# Plot range
ax.plot([n - 0.5, n + 0.5], [np.min(eigenvalues), np.min(eigenvalues)], 'k-', alpha=0.5) # Draw a line for the range
ax.plot([n - 0.5, n + 0.5], [np.max(eigenvalues), np.max(eigenvalues)], 'k-', alpha=0.5) # Draw a line for the range
ax.set_xlabel('Molecular formula')
ax.set_ylabel('Largest eigenvalue')
ax.set_xticks(range(1, 12))
ax.set_xticklabels([f'C{n}H{2*n + 2}' for n in range(1, 12)])
ax.set_title('Largest eigenvalues of the log-Coulomb matrix for alkane constitutional isomers')
plt.savefig('alkane_log_coulomb_matrix_largest_eigenvalues.webp', bbox_inches='tight')
Largest eigenvalues of the log-Coulomb matrix for alkane constitutional isomers.
Now, we see that the largest eigenvalues of the log-transformed Coulomb matrix have the potential to become much more dominated to by the hydrogen atoms. This results in a large negative magnitude for the largest eigenvalue.
What I find to be interesting is that the range of the distribution across isomers grows as we add more carbon atoms to the molecule. For some isomers, the carbon atom interactions remain dominant, but for others, the hydrogen atom interactions become dominant. This is in contrast to the original Coulomb matrix eigenvalues, where the range of the distribution across isomers grows sub-linearly with the number of carbon atoms in the molecule and hydrogen atom interactions are virtually irrelevant.
Figure 2 Redux - Maximum Eigenvalue PDFs for $C_7H_{16}$ and Its Constitutional Isomers
for n_sel in range(4, 8):
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
smiles = []
with open(f'isomers/C{n_sel}H{2*n_sel + 2}.smi') as f:
for line in f:
smiles.append(line.strip())
for i in range(len(log_spectra[n_sel])):
eigenvalues = log_spectra[n_sel][i][:, 0]
# kde plot with the following params
# - Gaussian kernel
# - bandwidth with Silverman's rule of thumb
# - log scale y-axis
ax = sns.kdeplot(eigenvalues, bw_method='silverman', label=get_iupac_name(smiles[i]), log_scale=(False, True))
ax.set_xlabel('Largest eigenvalue')
ax.set_ylabel('Density')
ax.set_title('PDF of the largest eigenvalue for $C_' + str(n_sel) + 'H_{' + str(2*n_sel + 2) + '}$')
ax.legend()
plt.savefig(f'pdf_log_largest_eigenvalue_C{n_sel}H{2*n_sel + 2}.webp', bbox_inches='tight')
plt.close()
PDFs of the largest eigenvalue for $C_7H_{16}$ and its constitutional isomers.
Here, I plot the PDFs of the largest eigenvalue for $C_7H_{16}$ and its constitutional isomers, but this time with a log scale on the y-axis. The reason is otherwise, the less branched isomers become invisible due to the more highly concentrated distributions of the more branched isomers.
In this, I think this exposes an issue of the log-transformation of the Coulomb matrix. The distributions can become a lot more wide and overlapping (as shown here).
Figure 3 Redux - 2D Space of Log-Transformed Coulomb Matrix Eigenvalues for $C_4H_{10}$ (Butane and Isobutane)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
n_sel = 4
smiles = []
with open(f'isomers/C{n_sel}H{2*n_sel + 2}.smi') as f:
for line in f:
smiles.append(line.strip())
for i in range(len(log_spectra[n_sel])):
eigenvalues = log_spectra[n_sel][i][:, :2]
ax.scatter(eigenvalues[:, 0], eigenvalues[:, 1], label=get_iupac_name(smiles[i]))
ax.set_xlabel('Largest eigenvalue')
ax.set_ylabel('Second largest eigenvalue')
ax.set_title('2D plot of the first two eigenvalues for $C_4H_{10}$ conformers')
ax.legend()
plt.savefig(f'2d_log_largest_eigenvalue_C{n_sel}H{2*n_sel + 2}.webp', bbox_inches='tight')
2D space of log-transformed Coulomb matrix eigenvalues for $C_4H_{10}$ (butane and isobutane).
While the two isomers have been brought closer together, not much of major substance has changed with this plot. We can still linearly separate the two isomers in 2D space using the first two eigenvalues of the log-transformed Coulomb matrix.
Figure 4 Redux - Number of Principal Components Required for 99% Variance in Log-Transformed Coulomb Matrix Eigenvalues
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
n_components = {}
for n in range(1, 12):
n_components[n] = []
for i in range(len(log_spectra[n])):
eigenvalues = log_spectra[n][i]
# PCA
pca = PCA(n_components=0.99, svd_solver='full', whiten=False, random_state=42)
pca.fit(eigenvalues)
n_components[n].append(pca.n_components_)
ax.scatter([n] * len(n_components[n]), n_components[n], alpha=0.3)
ax.plot([n - 0.25, n + 0.25], [np.mean(n_components[n]), np.mean(n_components[n])], 'k-', alpha=0.5) # Draw a line for the mean
ax.plot([1, 11], [1, 11], 'k--', alpha=0.5, label='y = num carbon')
ax.plot([1, 11], [5, 35], 'r--', alpha=0.5, label='y = num atoms')
ax.set_xlabel('Number of carbon atoms')
ax.set_ylabel('Number of principal components')
ax.set_title('99% variance explained by number of principal components')
plt.legend()
plt.savefig('99_variance_explained_log.webp', bbox_inches='tight')
99% variance explained by number of principal components for log-transformed Coulomb matrix eigenvalues.
The number of principal components required to explain 99% of the variance in the log-transformed Coulomb matrix eigenvalues is quite similar to the original Coulomb matrix eigenvalues, but is increased on average. This is intriguing, but may ultimately not be of practical use.
Conclusion
In this post, we’ve gone through the process of generating the constitutional isomers for alkanes, generating their 3D structures, calculating the Coulomb matrix, and calculating the eigenvalues of the Coulomb matrix. We’ve then validated our generation process by comparing the figures we’ve generated to the figures in the original paper.
If you enjoyed this post, consider:
- Reading a similar post, such as: Molecular Descriptor: Coulomb Matrix or Part Two of this series
- Sharing this post with a friend
- Buying me a coffee (see the button on the lower right)