When I first encountered multi-arm bandit problems, I was overwhelmed by the variety of approaches and terminology. While working through Bandit Algorithms by Tor Lattimore and Csaba Szepesvári, I realized what I needed was a simple framework to organize my thinking about these problems.

Note: I originally wrote this in 2020, but bandit algorithms have become even more relevant with LLMs, personalized AI systems, and real-time optimization.

The core idea is straightforward: imagine you’re at a casino with multiple slot machines. Each machine has different (unknown) payout rates. You want to maximize your winnings, but you don’t know which machines are best. Do you keep playing the machine that’s paid out well so far, or try others to see if they’re better? This is the exploration-exploitation dilemma at the heart of bandit algorithms.

Bandit algorithms solve this by learning the reward distributions for each arm over time, balancing the need to explore new options with exploiting what they’ve learned.

Illustration of a vintage slot machine with multiple arms, representing the multi-arm bandit problem in machine learning where algorithms must balance exploration and exploitation
Multi-arm bandit algorithms balance exploration and exploitation

What I’ve found helpful is thinking about any bandit problem along five key dimensions. This isn’t the only way to categorize these algorithms, but it’s helped me quickly identify which approaches might work for a given problem.

Flowchart diagram showing the five key dimensions for characterizing multi-arm bandit problems: action space, problem structure, external information, reward mechanism, and learner feedback
Questions to ask for bandit algorithms

Here are the five dimensions I find most useful for thinking about bandit problems:

  1. Action Space - Finite vs. infinite, single vs. combinatorial
  2. Problem Structure - Whether actions provide information about other actions
  3. External Information - Availability of contextual information
  4. Reward Mechanism - Stochastic, non-stationary, or adversarial
  5. Learner Feedback - Bandit, full, partial, or semi-bandit feedback

Jump to Real-World Applications to see these dimensions in practice.

Mathematical Notation Guide

Throughout this post, we use the following notation:

  • $k$ = number of arms/actions
  • $\theta$ = parameter of reward distribution
  • $t$ = time step or round
  • $X_t$ = reward received at time $t$
  • $\mathbb{E}[X]$ = expected value of random variable $X$

What Can You Do? (Action Space)

The first question is simple: what options do you have?

Few Options vs. Many Options

Most people think of bandit problems as choosing between a small number of discrete options—maybe 5 different website layouts or 3 different ad campaigns. This is the straightforward case.

But sometimes your “action” has continuous parameters. Maybe you’re setting a bid price anywhere from $0.01 to $10.00, or adjusting a recommendation algorithm’s temperature parameter. Suddenly you have infinite possible actions, which requires different approaches (usually involving assumptions about how similar actions perform similarly).

One Choice vs. Multiple Choices

Sometimes you pick just one option (show this ad), but other times you select multiple things at once (which 10 movies to recommend on Netflix’s homepage). The multi-choice case is trickier because your selections might interact—maybe showing two similar movies together is worse than showing them separately.

Summary

Action spaces can be characterized along two key dimensions:

  • Size: Finite (select from $k$ discrete options) vs. infinite (continuous parameter selection)
  • Complexity: Single action vs. combinatorial action selection

Understanding your action space is crucial as it determines which algorithmic approaches are feasible and what theoretical guarantees you can expect.

Visual diagram illustrating the two dimensions of action spaces in bandit problems: finite vs infinite actions, and single vs combinatorial action selection
Bandit action space distinctions

Do Your Choices Tell You About Other Choices? (Problem Structure)

This is often overlooked but crucial: does trying option A teach you anything about option B?

In many problems, each choice is completely independent. Testing email marketing tells you nothing about social media campaigns—they’re just different.

But sometimes there are patterns. If you’re testing discount amounts (10% vs 15% vs 20% off), learning that 10% works well gives you hints about whether 15% might be worth the extra cost. The key insight is whether your problem has some underlying structure you can exploit.

What Extra Information Do You Have? (Context)

Real-world problems rarely happen in isolation. Maybe your website performs differently on weekdays vs weekends, or your recommendation system should consider user demographics.

The question is: what additional information might help you make better decisions?

Sometimes it’s environmental (time of day, season, device type). Sometimes it’s about the user (age, location, past behavior). The key is identifying information that actually predicts performance and incorporating it into your decision-making.

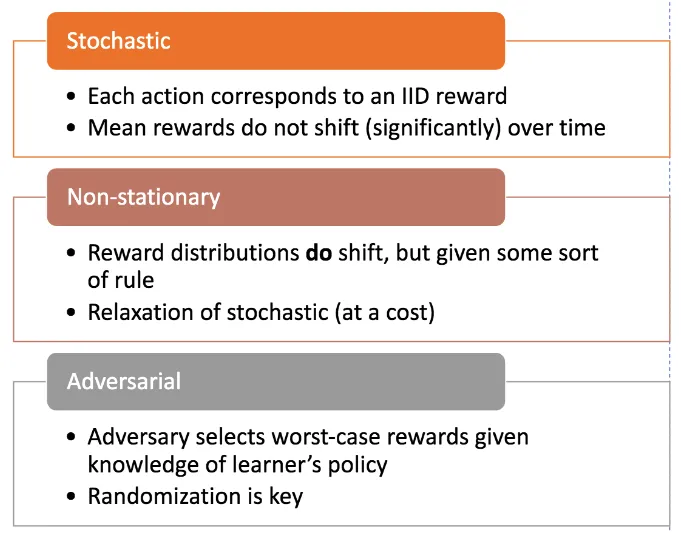
How Do Rewards Work? (Reward Mechanism)

This dimension is about understanding the nature of the feedback you’re getting. Are the rewards predictable, changing over time, or actively working against you?

Stable but Random (Stochastic)

This is the “normal” case—each option has some underlying performance level, but you see random variation around it. Like clinical trials where a drug has a true effectiveness rate, but individual patients respond differently.

Things Change Over Time (Non-Stationary)

Sometimes the world shifts under your feet. What worked last month might not work this month. Stock trading is a classic example—market conditions change constantly, so you need algorithms that can adapt.

Someone’s Working Against You (Adversarial)

In the worst case, something is actively trying to make your algorithm fail. This happens in cybersecurity where attackers adapt to your defenses. It requires fundamentally different approaches, usually involving some randomness to stay unpredictable.

Comparison chart showing three types of reward mechanisms in bandit problems: stochastic rewards with fixed distributions, non-stationary rewards that change over time, and adversarial rewards selected to minimize algorithm performance
Bandit reward mechanisms

How Much Do You Learn From Each Decision? (Feedback)

The last dimension is about information—how much do you learn each time you make a choice?

Just Your Choice (Bandit Feedback)

This is the classic case: you pick option A and only learn how A performed. You have no idea what would have happened if you’d picked B. This creates the exploration-exploitation tension that makes bandits interesting.

Everything (Full Feedback)

Sometimes you can see how all options would have performed. This happens when you’re analyzing historical data—like looking back at stock prices where you can see what every possible investment would have returned.

Something In Between (Partial Feedback)

This is common when you’re choosing multiple things at once. Maybe you’re running several ads and can see how each individual ad performed, not just the overall campaign. This extra information can be really valuable for learning faster.

Information flow diagram showing different feedback types in bandit algorithms: bandit feedback (single action reward), full feedback (all action rewards), partial feedback (subset of rewards), and semi-bandit feedback (combinatorial sub-action rewards)
Bandit feedback scenarios

Real Examples

Here’s how these dimensions play out in practice:

E-commerce Recommendations

  • What can you do? Pick multiple products to show (combinatorial)
  • Do choices relate? Yes, similar products perform similarly (structured)
  • Extra info? Lots—user history, time of day, device type
  • How do rewards work? Pretty stable user preferences (stochastic)
  • What do you learn? Only see clicks on what you showed (bandit feedback)

Online Ad Bidding

  • What can you do? Bid any amount from $0.01 to $10 (infinite actions)
  • Do choices relate? Yes, similar bids perform similarly (structured)
  • Extra info? User demographics, search terms, ad relevance
  • How do rewards work? Market conditions change constantly (non-stationary)
  • What do you learn? Only results from your winning bids (bandit feedback)

Content Personalization

  • What can you do? Select articles/videos for homepage (combinatorial)
  • Do choices relate? Content categories have patterns (structured)
  • Extra info? User profile, trends, browsing history
  • How do rewards work? User interests evolve over time (non-stationary)
  • What do you learn? Performance of individual content pieces (partial feedback)

A Practical Decision Guide

When I encounter a new bandit problem, I work through these questions in order:

Step 1: What are my options?

  • Few discrete choices? → Try UCB or Thompson Sampling
  • Continuous parameters? → Look into Gaussian Process methods

Step 2: Do my choices relate to each other?

  • Yes? → Use linear bandits or kernel methods to share information
  • No? → Treat each option independently

Step 3: What extra information do I have?

  • Rich context? → Use contextual bandits (LinUCB works well)
  • No context? → Stick with standard approaches

Step 4: How do rewards behave?

  • Stable? → UCB and Thompson Sampling work great
  • Changing over time? → Add forgetting factors or use sliding windows
  • Someone working against me? → Need adversarial approaches like EXP3

Step 5: How much do I learn each time?

  • Just my choice? → Standard bandit algorithms
  • Everything? → Online gradient descent or multiplicative weights
  • Something in between? → Exploit the extra structure

This isn’t the only way to think about these problems, but it’s helped me avoid getting lost in the academic literature and focus on what actually matters for the problem at hand.

Summary

These five questions have helped me navigate bandit problems more systematically:

  1. What can you do? (Action space: few vs many options, single vs multiple choices)
  2. Do choices relate? (Whether trying one option teaches you about others)
  3. What extra info do you have? (Context that might improve decisions)
  4. How do rewards work? (Stable, changing, or adversarial)
  5. How much do you learn? (Feedback from just your choice vs everything)

The framework isn’t perfect, but it’s helped me avoid getting overwhelmed by the academic literature and focus on what matters for real problems. Structured problems let you learn faster by sharing information between options, while adversarial settings require completely different approaches.

If You Want to Learn More