What kind of paper is this?
This is a Methodological ($\Psi_{\text{Method}}$) paper. It introduces a “general nonlinear logit model” and a specific estimation algorithm (NOMINATE) to analyze political choice data. The paper focuses on deriving a metric spatial map from nominal data (yea/nay votes). It validates this method by comparing it against existing “state-of-the-art” techniques like Guttman scaling and factor analysis, demonstrating that the new method recovers geometric structures that previous methods obscured.
What is the motivation?
Prior research relied on “black box” statistical methods (like factor analysis or nonmetric scaling) or Guttman scaling to analyze legislative behavior. These methods had significant limitations:
- Metric Recovery: They struggled to accurately recover the underlying Euclidean coordinates of legislators and choices from nominal data.
- Dimensionality: They tended to exaggerate the number of dimensions (issues) because they did not account for probabilistic error in voting.
- Identification: Pure Guttman scaling (assuming perfect voting) identifies only the order of legislators, leaving the location of policy alternatives unknown.
The authors sought to bridge the “crucial gap” between spatial theory and data by developing a model-driven procedure that simultaneously estimates the locations of choosers and choices while accounting for error.
What is the novelty here?
The core contribution is the NOMINATE (Nominal Three-step Estimation) procedure. Key innovations include:
- Simultaneous Estimation: This method estimates coordinates for both the legislators ($x_i$) and the roll call outcomes ($z_{jl}$) in a common space simultaneously.
- Probabilistic Utility: It employs a specific bell-shaped utility function with a stochastic error term (log of the inverse exponential), allowing for a tractable probabilistic voting model.
- Metric Unfolding: It successfully performs “unfolding methodology for nominal level data,” recovering metric distances solely from binary choices.
What experiments were performed?
The authors validated the model through both historical data analysis and synthetic testing:
- US House Analysis (1957-58): Analyzed 172 roll calls from the 85th Congress to compare NOMINATE results against Miller and Stokes’ influential Guttman scales.
- US Senate Analysis (1979-1982): Performed separate estimations for four years of Senate voting to assess stability and validity.
- Monte Carlo Simulations: Generated synthetic data using random numbers to test the robustness of parameter recovery under known “truth” conditions.
- Robustness Checks: Tested sensitivity to “perfect” legislators (who never vote against their side) and outliers (like Senator Proxmire).
What outcomes/conclusions?
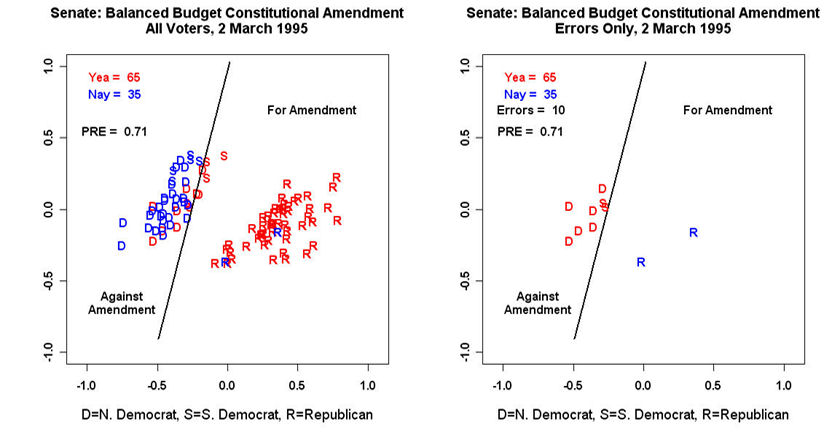
- Unidimensionality: A single liberal-conservative dimension correctly classified ~80% of individual choices in the US House and Senate.
- Methodological Superiority: The model demonstrated that distinct “issue scales” found in previous research (e.g., social welfare vs. foreign policy) could largely be mapped onto a single dimension when error is accounted for.
- Strategic Behavior: The analysis revealed that majority leadership tends to place roll call midpoints slightly away from the median legislator to increase the probability of passage.
- Geometric Mean Probability: The authors introduced the geometric mean probability as a more robust metric than simple classification error for evaluating probabilistic models.
Reproducibility Details
Data
The paper analyzes roll call voting matrices where rows are legislators and columns are roll calls.
| Context | Size | Details |
|---|---|---|
| US House (85th) | 440 Legislators x 172 Roll Calls | 68,284 choices; 1957-58 |
| US Senate | ~100 Senators/year | Years 1979, 1980, 1981, 1982 |
| Filtering | Cutoff > 2.5% | Roll calls with < 2.5% minority vote are excluded to prevent “noise” from distorting estimates. |
Algorithms
The NOMINATE algorithm maximizes the log-likelihood of observed choices using a constrained nonlinear maximum likelihood procedure.
Utility Function: The utility of legislator $i$ for outcome $j$ on roll call $l$ is: $$U_{ijl}=\beta~\exp\left[\frac{-\omega^{2}d_{ijl}^{2}}{2}\right]+\epsilon_{ijl}$$ Where $d_{ijl}$ is the Euclidean distance between legislator $i$ and outcome $j$.
Optimization Strategy (Global Iteration): Because estimating ~800 parameters simultaneously is impractical, the algorithm uses an alternating three-step method:
- Utility Parameters: Estimate $\beta$ and $\omega$ while holding legislator ($x$) and roll call ($z$) coordinates fixed.
- Legislator Coordinates: Estimate $x_i$ for each legislator (independent of others) holding $\beta, \omega, z$ fixed.
- Roll Call Coordinates: Estimate $z_{yl}, z_{nl}$ for each roll call holding $\beta, \omega, x$ fixed.
This cycle repeats until parameters correlate at the 0.99 level between iterations.
Models
The model estimates the following parameters for a one-dimensional space:
- Legislator Coordinates ($x_i$): The ideal point of each legislator, normalized to the range $[-1, +1]$.
- Outcome Coordinates ($z_{yl}, z_{nl}$): The spatial location of the “Yea” and “Nay” policy outcomes for each vote.
- Signal-to-Noise ($\beta$): Represents the weight of the spatial component versus the error term.
- Weighting ($\omega$): A shape parameter for the utility function (often fixed to $0.5$ in practice due to collinearity with $\beta$).
Evaluation
Performance is evaluated primarily via classification accuracy and probabilistic fit.
| Metric | Value | Context | Notes |
|---|---|---|---|
| Classification | 78.9% | House (1957-58) | Correctly predicts Yea/Nay choice |
| Classification | ~80-83% | Senate (1979-82) | |
| Geo. Mean Prob. | ~0.64 - 0.66 | Aggregate | Exponential of the average log likelihood |
Hardware
- Development: DEC-2060
- Production: VAX-11/780
Paper Information
Citation: Poole, K. T., & Rosenthal, H. (1985). A Spatial Model for Legislative Roll Call Analysis. American Journal of Political Science, 29(2), 357-384. https://doi.org/10.2307/2111172
Publication: American Journal of Political Science 1985
@article{pooleSpatialModelLegislative1985,
title = {A {{Spatial Model}} for {{Legislative Roll Call Analysis}}},
author = {Poole, Keith T. and Rosenthal, Howard},
year = 1985,
journal = {American Journal of Political Science},
volume = {29},
number = {2},
pages = {357--384},
doi = {10.2307/2111172}
}
Additional Resources: