Funnels, Pathways, and Energy Landscapes

Paper Information

Citation: Bryngelson, J. D., Onuchic, J. N., Socci, N. D., & Wolynes, P. G. (1995). Funnels, Pathways, and the Energy Landscape of Protein Folding: A Synthesis. Proteins: Structure, Function, and Genetics, 21(3), 167-195. https://doi.org/10.1002/prot.340210302

Publication: Proteins 1995

Additional Resources:

• How to Fold Graciously: Levinthal’s 1969 Paradox
• Wikipedia: Energy landscape
• Levinthal’s Paradox

What kind of paper is this?

This is primarily a Theory paper ($\Psi_{\text{Theory}}$) with a strong Systematization component ($\Psi_{\text{Systematization}}$).

• Theory: It applies statistical mechanics (specifically spin glass theory) to derive formal relationships between energy barriers, entropy, and folding kinetics.
• Systematization: It synthesizes two previously conflicting views—specific “folding pathways” versus thermodynamic “funnels”—into a unified phase diagram.

What is the motivation?

The work addresses Levinthal’s Paradox: the disconnect between the astronomical number of possible conformations (requiring $10^{10}$ years to search randomly) and the millisecond-to-second timescales observed in biology.

• The Conflict: Previous theories relied on specific, unique folding pathways (Levinthal’s solution) or distinct intermediates. The authors argue these are insufficient to explain the robustness of folding.
• The Gap: There was a need to quantitatively distinguish between sequences that fold reliably (“good folders”) and random heteropolymers that get trapped in local minima (glassy states).

What is the novelty here?

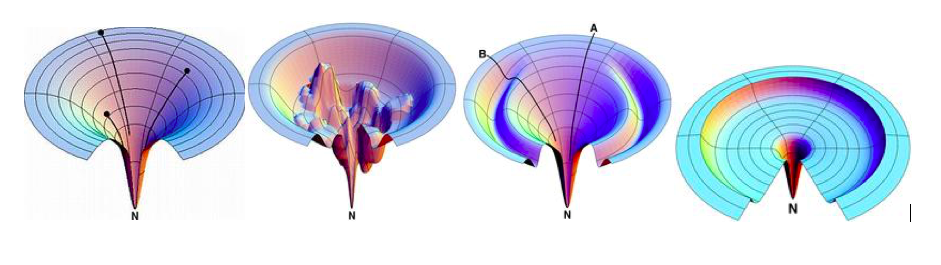
The core novelty is the Energy Landscape Theory, which posits that proteins fold via a “funnel” rather than a single pipe-like pathway.

• Folding Funnel: A landscape where the energy generally decreases as the protein gets structurally closer to the native state (similarity $n$).
• Principle of Minimal Frustration: Natural proteins are evolved to minimize conflicting interactions (frustration), creating a smooth funnel that guides the chain to the native state.
• Stability Gap: The relevant energy gap is not between the ground state and the next state, but between the native state and the average energy of the “molten globule” or disordered compact states. Maximizing this gap ($T_f / T_g$) ensures foldability.
• Folding Scenarios: The definition of distinct kinetic scenarios (Type 0, Type I, Type II) based on the relationship between the folding temperature ($T_f$) and the glass transition temperature ($T_g$).

What experiments were performed?

The authors performed analytical derivations and lattice simulations to validate the theory.

• Lattice Simulations: They simulated 27-mer heteropolymers on a cubic lattice using Monte Carlo methods.
• Sequence Variation: They compared “designed” sequences (unfrustrated) against random sequences to observe differences in collapse and folding times.
• Phase Diagram Mapping: They mapped the behavior of these polymers onto a Phase Diagram (Temperature vs. Landscape Roughness $\Delta E$), predicting regions of random coil, globule, folded, and glass states.

What were the outcomes and conclusions drawn?

• Folding is Ensemble-Based: Folding is not a search for a single path but a “funneling” of an ensemble of conformations toward the native state.
• Glass Transition: If the landscape is too rough (high frustration), the protein enters a “glassy” phase ($T < T_g$) where kinetics become non-exponential and non-self-averaging (highly sensitive to sequence details).
• Curved Arrhenius Plots: The theory predicts that Arrhenius plots (rate vs. $1/T$) will be curved (parabolic) due to the temperature dependence of the entropic search on a rough landscape, matching experimental observations.
• Optimization Criterion: To engineer fast-folding proteins, one must maximize the stability gap ratio ($T_f/T_g$), effectively separating the native state from the bulk of compact disordered states.

Reproducibility Details

The simulations are based on the “27-mer” cubic lattice model, a standard paradigm in theoretical protein folding.

Data

The “data” consists of specific synthetic sequences used in the Monte Carlo simulations.

• Source: Table I in the paper.
• Alphabet: Two-letter code (A/B), representing hydrophobic/polar distinctions.

Algorithms

• Simulation Method: Monte Carlo (MC) sampling on a discrete lattice.
• Glass Transition ($T_g$) Definition: Defined kinetically where the folding time $\tau_f(T_g)$ exceeds $(\tau_{max} + \tau_{min})/2$. In this study, $\tau_{max} = 1.08 \times 10^9$ MC steps.
• Folding Temperature ($T_f$): Calculated using the Monte Carlo histogram method, defined as the temperature where the probability of occupying the native structure is 0.5.

Models

• Lattice: 27 monomers on a $3 \times 3 \times 3$ cubic lattice (maximally compact states can be fully enumerated).
• Potential Energy:
  • Interactions occur between nearest neighbors on the lattice that are not covalently connected.
  • $E_{AA} = E_{BB} = -3$ (Strong attraction for like pairs).
  • $E_{AB} = -1$ (Weak attraction for unlike pairs).
• Frustration: Defined via the $Q$ measure (similarity to ground state). “Frustrated” sequences have low-energy states that are structurally dissimilar (low $Q$) to the ground state.

Evaluation

• Folding Time ($\tau$): Mean first passage time (MFPT) to reach the native structure from a random coil.
• Collapse Time: Time required to reach a conformation with 25 or 28 contacts for the first time.
• Reaction Coordinate: The similarity measure $n$ (or $Q$), typically defined as the number of native contacts formed.

Citation

@article{bryngelson1995funnels,
  title={Funnels, Pathways, and the Energy Landscape of Protein Folding: A Synthesis},
  author={Bryngelson, Joseph D. and Onuchic, José Nelson and Socci, Nicholas D. and Wolynes, Peter G.},
  journal={Proteins: Structure, Function, and Genetics},
  volume={21},
  number={3},
  pages={167--195},
  year={1995},
  doi={10.1002/prot.340210302}
}