Paper Information
Citation: Weiler, M., Geiger, M., Welling, M., Boomsma, W., & Cohen, T. S. (2018). 3D steerable CNNs: Learning rotationally equivariant features in volumetric data. Advances in Neural Information Processing Systems, 31. https://proceedings.neurips.cc/paper/2018/hash/488e4104520c6aab692863cc1dba45af-Abstract.html
Publication: NeurIPS 2018
Additional Resources:
What kind of paper is this?
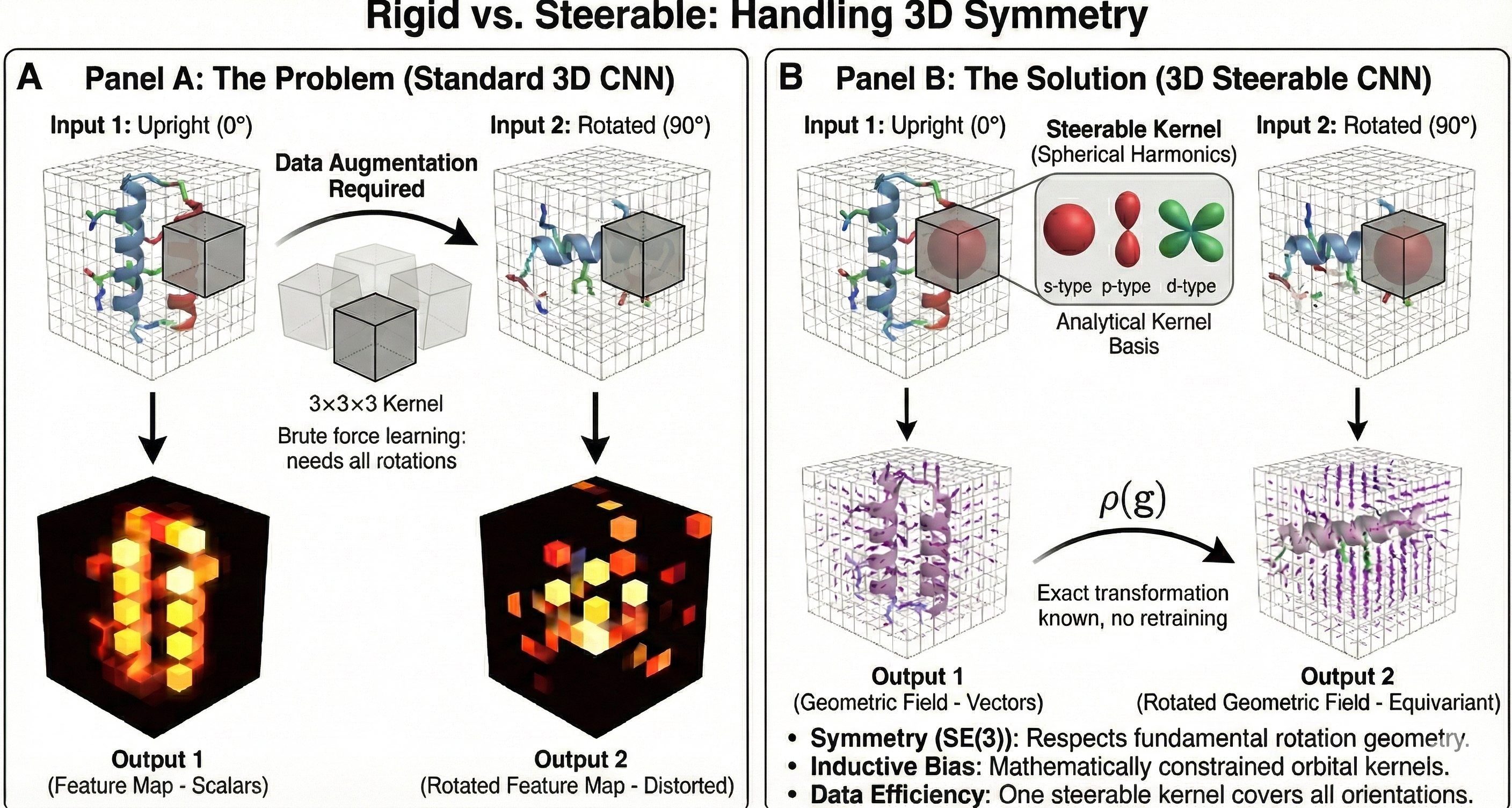
This is a method paper that introduces a novel neural network architecture, the 3D Steerable CNN. It provides a comprehensive theoretical derivation for the architecture grounded in group representation theory and demonstrates its practical application.
What is the motivation?
The work is motivated by the prevalence of symmetry in problems from the natural sciences. Standard 3D CNNs are not inherently equivariant to 3D rotations, a fundamental symmetry governed by the SE(3) group in many scientific datasets like molecular or protein structures. Building this symmetry directly into the model architecture as an inductive bias is expected to yield more data-efficient, generalizable, and physically meaningful models.
What is the novelty here?
The core novelty is the rigorous and practical construction of a CNN architecture that is equivariant to 3D rigid body motions (SE(3) group). The key contributions are:
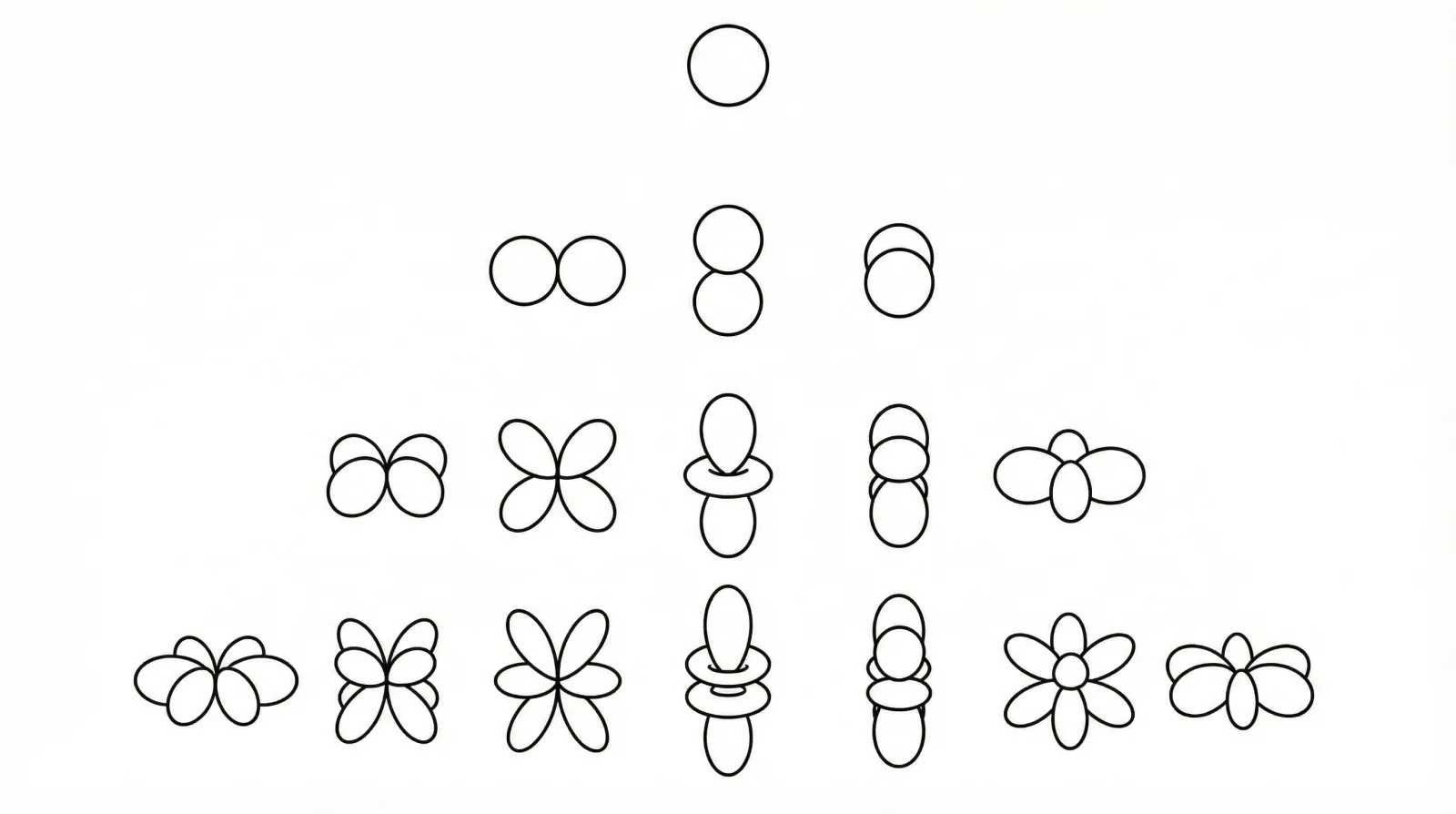
- Geometric Feature Representation: Features are modeled as geometric fields (collections of scalars, vectors, and higher-order tensors) defined over $\mathbb{R}^{3}$. Each type of feature transforms according to an irreducible representation (irrep) of the rotation group SO(3).
- General Equivariant Convolution: The paper proves that the most general form of an SE(3)-equivariant linear map between these fields is a convolution with a rotation-steerable kernel.
- Analytical Kernel Basis: The main theoretical breakthrough is the analytical derivation of a complete basis for these steerable kernels. They solve the kernel’s equivariance constraint, $\kappa(rx) = D^{j}(r)\kappa(x)D^{l}(r)^{-1}$, showing the solutions are functions whose angular components are spherical harmonics. The network’s kernels are then parameterized as a learnable linear combination of these pre-computed basis functions, making the implementation a minor modification to standard 3D convolutions.
- Equivariant Nonlinearity: A novel gated nonlinearity is proposed for non-scalar features. It preserves equivariance by multiplying a feature field by a separately computed, learned scalar field (the gate).
What experiments were performed?
The model’s performance was evaluated on a series of tasks with inherent rotational symmetry:
- Tetris Classification: A toy problem to empirically validate the model’s rotational equivariance by training on aligned blocks and testing on randomly rotated ones.
- SHREC17 3D Model Classification: A benchmark for classifying complex 3D shapes that are arbitrarily rotated.
- Amino Acid Propensity Prediction: A scientific application to predict amino acid types from their 3D atomic environments.
- CATH Protein Structure Classification: A challenging task on a new dataset introduced by the authors, requiring classification of global protein architecture, a problem with full SE(3) invariance.
What were the outcomes and conclusions drawn?
The 3D Steerable CNN demonstrated significant advantages due to its built-in equivariance:
- It was empirically confirmed to be rotationally equivariant, achieving 99% test accuracy on the rotated Tetris dataset, whereas a standard 3D CNN failed with 27% accuracy.
- It achieved state-of-the-art results on the amino acid prediction task and performed competitively on the SHREC17 benchmark, all while using significantly fewer parameters than the baseline models.
- On the CATH protein classification task, it dramatically outperformed a deep 3D CNN baseline despite having over 100 times fewer parameters. This performance gap widened as the training data was reduced, highlighting the model’s superior data efficiency.
The paper concludes that 3D Steerable CNNs provide a universal and effective framework for incorporating SE(3) symmetry into deep learning models, leading to improved accuracy and efficiency for tasks involving volumetric data, particularly in scientific domains.
Technical Implementation Details
Data Preprocessing
- Input Format: All inputs must be voxelized. Point clouds are not used directly.
- Proteins (CATH): $50^3$ grid, 0.2 nm voxel size. Gaussian density placed at atom centers.
- 3D Objects (SHREC17): $64^3$ voxel grids.
- Tetris: $36^3$ input grid.
- Splitting Strategy: CATH used a 10-fold split (7 train, 1 val, 2 test) strictly separated by “superfamily” level to ensure no data leakage (<40% sequence identity).
Architecture Specifications
Kernel Basis Construction:
- Constructed from Spherical Harmonics multiplied by Gaussian Radial Shells: $\exp\left(-\frac{1}{2}(||x||-m)^{2}/\sigma^{2}\right)$
- Anti-aliasing: A radially dependent angular frequency cutoff ($J_{\max}$) is applied to prevent aliasing near the origin.
Normalization: Uses Equivariant Batch Norm. Non-scalar fields are normalized by the average of their norms.
Downsampling: Standard strided convolution performs poorly. Must use low-pass filtering (Gaussian blur) before downsampling to maintain equivariance.
Hyperparameters & Training
| Parameter | Value |
|---|---|
| Optimizer | Adam |
| LR Scheduler | Exponential decay (0.94/epoch) after 40 epoch burn-in |
| Dropout (CATH) | 0.1 (Capsule-wide convolutional dropout) |
| Weight Decay (CATH) | L1 & L2 regularization: $10^{-8.5}$ |
Mathematical Formulations for Equivariance
Standard operations like Batch Normalization and ReLU break rotational equivariance. The paper derives equivariant alternatives:
Equivariant Batch Normalization:
Standard BN subtracts a mean, which introduces a preferred direction and breaks symmetry. Instead, use norm-based normalization that scales feature fields by the average of their squared norms:
$$f_{i}(x) \mapsto f_{i}(x) \left( \frac{1}{|B|} \sum_{j \in B} \frac{1}{V} \int dx |f_{j}(x)|^{2} + \epsilon \right)^{-1/2}$$
This scales vector lengths to unit variance on average without subtracting a mean, preserving directional information and symmetry.
Equivariant Nonlinearities:
You cannot apply ReLU to vector components independently (this depends on the coordinate frame). Two approaches:
Norm Nonlinearity (geometric shrinking): Acts on magnitude, preserves direction. Shrinks vectors shorter than learned bias $\beta$ to zero: $$f(x) \mapsto \text{ReLU}(|f(x)| - \beta) \frac{f(x)}{|f(x)|}$$ Note: Found to converge slowly; not used in final models.
Gated Nonlinearity (used in practice): A separate scalar field $s(x)$ passes through sigmoid to create a gate $\sigma(s(x))$, which multiplies the geometric field: $$f_{\text{out}}(x) = f_{\text{in}}(x) \cdot \sigma(s(x))$$ Architecture implication: Requires extra scalar channels ($l=0$) solely for gating higher-order channels ($l>0$).
Voxelization Details:
For CATH protein inputs, Gaussian density is placed at each atom position with standard deviation equal to half the voxel width ($0.5 \x0.2\text{ nm} = 0.1\text{ nm}$).
Exact Architecture Configurations
Tetris Architecture (4 layers):
| Layer | Field Types | Spatial Size |
|---|---|---|
| Input | - | $36^3$ |
| Layer 1 | 4 scalars, 4 vectors ($l=1$), 4 tensors ($l=2$) | $40^3$ |
| Layer 2 | 16 scalars, 16 vectors, 16 tensors | $22^3$ (stride 2) |
| Layer 3 | 32 scalars, 16 vectors, 16 tensors | $13^3$ (stride 2) |
| Output | 8 scalars (global average pool) | - |
SHREC17 Architecture (8 layers):
| Layers | Field Types |
|---|---|
| 1-2 | 8 scalars, 4 vectors, 2 tensors ($l=2$) |
| 3-4 | 16 scalars, 8 vectors, 4 tensors |
| 5-7 | 32 scalars, 16 vectors, 8 tensors |
| 8 | 512 scalars |
| Output | 55 scalars (classes) |
CATH Architecture (ResNet34-inspired):
Block progression: (2,2,2,2) → (4,4,4) → (8,8,8,8) → (16,16,16,16)
Notation: (a,b,c,d) = $a$ scalars ($l=0$), $b$ vectors ($l=1$), $c$ rank-2 tensors ($l=2$), $d$ rank-3 tensors ($l=3$).
Quantitative Results
| Task | Metric | Steerable CNN | Baseline |
|---|---|---|---|
| Tetris (rotated test) | Accuracy | 99% | 27% (standard 3D CNN) |
| Amino Acid Propensity | Accuracy | 0.58 | 0.50 |
| SHREC17 | micro/macro MAP | 1.11 | 1.13 (SOTA) |
| CATH | Accuracy | Significantly higher | Deep 3D CNN (100x more params) |
Note: On SHREC17, the model performed comparably to SOTA, while using fewer parameters.
Historical Context (From Peer Reviews)
The NeurIPS peer reviews reveal important context about the paper’s structure and claims:
Evolution of Experiments: The SHREC17 experiment and the arbitrary rotation test in Tetris were added during the rebuttal phase to address reviewer concerns about the lack of standard computer vision benchmarks. This explains why SHREC17 feels somewhat disconnected from the paper’s “AI for Science” narrative.
Continuous vs. Discrete Rotations: The Tetris experiment validates equivariance to continuous ($SO(3)$) rotations alongside discrete 90-degree turns. This distinction is crucial and separates Steerable CNNs from earlier Group CNNs that only handled discrete rotation groups.
Terminology Warning: The use of terms like “fiber” and “induced representation” was critiqued by reviewers as being denser than necessary and inconsistent with related work (e.g., Tensor Field Networks). If you find Section 3 difficult, this is a known barrier of this paper. Focus on the resulting kernel constraints.
Parameter Efficiency Quantified: Reviewers highlighted that the main practical win is parameter efficiency. Standard 3D CNNs hit diminishing returns around $10^7$ parameters, whereas Steerable CNNs achieve better results with ~100x fewer parameters ($10^5$).
