Paper Information
Citation: Vincent, P. (2011). A Connection Between Score Matching and Denoising Autoencoders. Neural Computation, 23(7), 1661-1674. https://doi.org/10.1162/NECO_a_00142
Publication: Neural Computation 2011
Additional Resources:
What kind of paper is this?
This is a Theoretical Paper ($\Psi_{\text{Theory}}$).
Its primary contribution is a formal mathematical derivation connecting two previously distinct techniques: Score Matching (SM) and Denoising Autoencoders (DAE). It provides the “why” behind the empirical success of DAEs by grounding them in the probabilistic framework of energy-based models. It relies on proofs and equivalence relations (e.g., $J_{ESMq_{\sigma}} \sim J_{DSMq_{\sigma}}$)
What is the motivation?
The paper bridges a gap between two successful but disconnected approaches in unsupervised learning:
- Denoising Autoencoders (DAE): Empirically successful for pre-training deep networks but lacked a clear probabilistic interpretation (unlike Restricted Boltzmann Machines).
- Score Matching (SM): A theoretically sound method for estimating unnormalized density models that avoids the partition function problem but requires computing expensive second derivatives.
By connecting them, the authors aim to define a proper probabilistic model for DAEs (allowing sampling/ranking) and find a simpler way to apply score matching that avoids second derivatives.
What is the novelty here?
The core novelty is the Denoising Score Matching (DSM) framework and the proof of its equivalence to DAEs. Key contributions include:
- Equivalence Proof: Showing that training a DAE with Gaussian noise is equivalent to matching the score of a model against a non-parametric Parzen density estimator of the data.
- Denoising Score Matching ($J_{DSM}$): A new objective that learns a score function by trying to denoise corrupted samples. This avoids the explicit second derivatives required by standard Implicit Score Matching ($J_{ISM}$).
- Explicit Energy Function: Deriving the specific energy function $E(x;\theta)$ that corresponds to the standard sigmoid DAE architecture.
- Justification for Tied Weights: Providing a theoretical justification for tying encoder and decoder weights, which arises naturally from differentiating the energy function.
What experiments were performed?
As a theoretical paper, “experiments” in the traditional sense (benchmarks, datasets) are not the focus. The validation is mathematical:
- Derivation of Equivalence: The paper formally proves the chain of equivalences: $$J_{ISMq_{\sigma}} \sim J_{ESMq_{\sigma}} \sim J_{DSMq_{\sigma}} \sim J_{DAE\sigma}$$ where $q_{\sigma}$ is the Parzen density estimate.
- Appendix Proof: A detailed proof is provided to show that Explicit Score Matching ($J_{ESM}$) on the Parzen density is equivalent to the proposed Denoising Score Matching ($J_{DSM}$) objective.
What outcomes/conclusions?
- Theoretical Unification: DAE training is formally equivalent to Score Matching on a smoothed data distribution ($q_{\sigma}$).
- New Training Objective: The $J_{DSM}$ objective offers a computationally efficient way to perform score matching (no Hessian required) by using a denoising objective.
- Probabilistic Interpretation: DAEs can now be understood as Energy-Based Models (EBMs), allowing for operations like sampling (via Hybrid Monte Carlo) and likelihood ranking, which were previously ill-defined for standard autoencoders.
- Regularization Insight: The smoothing kernel width $\sigma$ in the Parzen estimator corresponds to the noise level in the DAE. This suggests that DAEs are learning a regularized version of the score, which may explain their robustness.
Key Concepts Explained
1. “Score” and “Score Matching”
What does “score” actually mean?
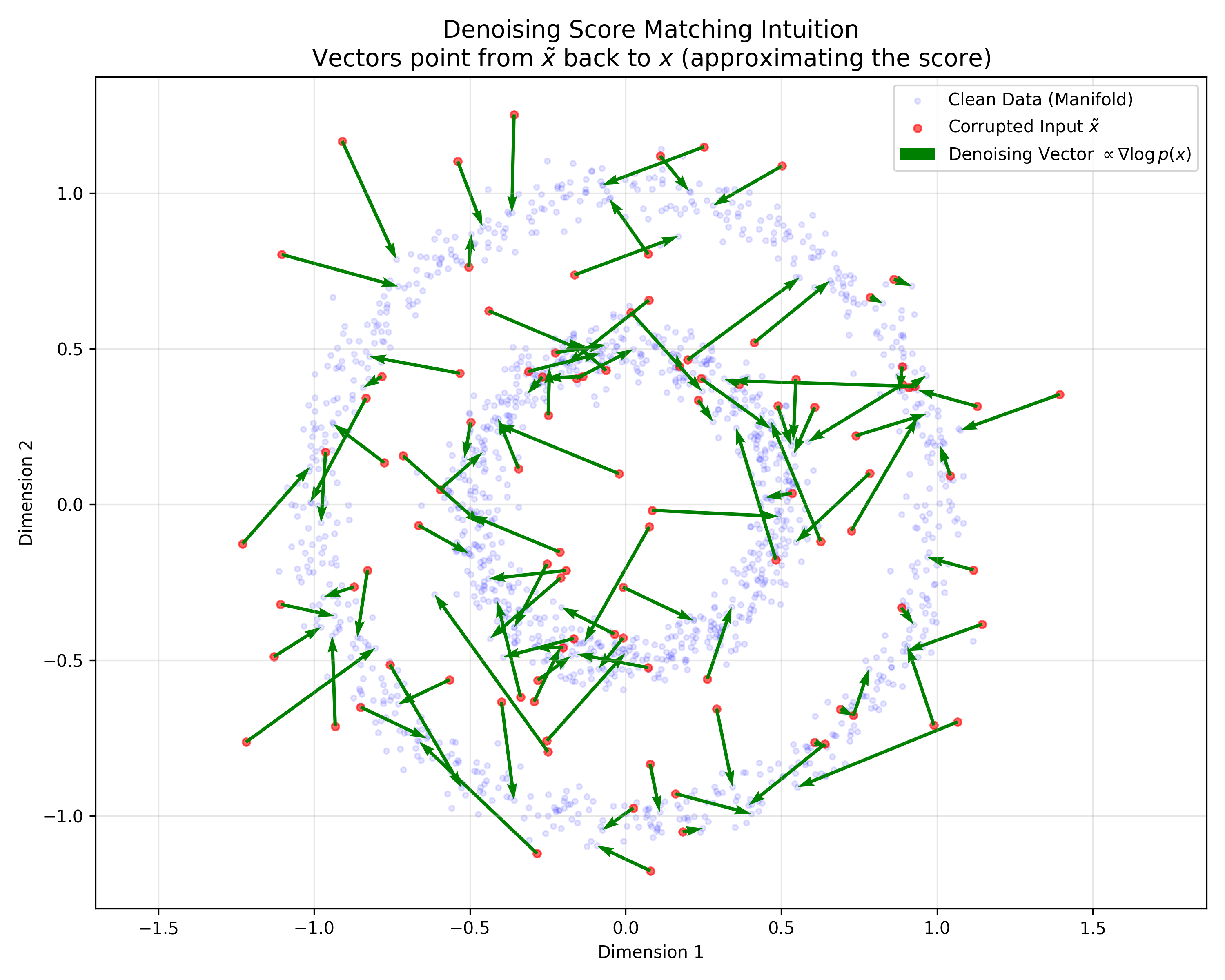
In this paper (and probabilistic modeling generally), the score is the gradient of the log-density with respect to the data vector $x$, not the parameters.
- Definition: $\psi(x) = \nabla_x \log p(x)$.
- Intuition: It is a vector field pointing in the direction of highest probability increase. Crucially, calculating the score does not require the intractable partition function $Z$, because $\nabla_x \log p(x) = \nabla_x \log \tilde{p}(x) - \nabla_x \log Z = \nabla_x \log \tilde{p}(x)$. The constant $Z$ vanishes upon differentiation.
What is Score Matching?
Score Matching is a training objective for unnormalized models. It minimizes the squared Euclidean distance between the model’s score $\psi(x;\theta)$ and the data’s true score $\nabla_x \log q(x)$.
2. The Parzen Density Estimator
What is it?
It is a non-parametric method for estimating a probability density function from finite data. It places a smooth kernel (here, a Gaussian) centered at every data point in the training set $D_n$.
- Formula: $q_{\sigma}(\tilde{x}) = \frac{1}{n} \sum_{t=1}^n \mathcal{N}(\tilde{x}; x^{(t)}, \sigma^2 I)$.
Why smooth the data?
To define the score: The empirical data distribution is a set of Dirac deltas (spikes). The gradient (score) of a Dirac delta is undefined. Smoothing creates a differentiable surface, allowing a valid target score $\nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x})$ to be computed.
To model corruption: The Parzen estimator with Gaussian kernels mathematically models the process of taking a clean data point $x$ and adding Gaussian noise - the exact procedure used in Denoising Autoencoders.
3. Why avoiding second derivatives matters
Standard Implicit Score Matching (ISM) eliminates the need for the unknown data score, but introduces a new cost: it requires computing the trace of the Hessian (the sum of second partial derivatives) of the log-density.
- The Cost: For high-dimensional data (like images) and deep networks, computing second derivatives is computationally prohibitive ($O(d^2)$ operations per sample).
- The Breakthrough: This paper shows that Denoising Score Matching (DSM) allows you to bypass Hessian computation entirely. By using the Parzen target, the objective simplifies to matching a first-order vector, making it scalable to deep neural networks.
4. The equivalence chain - why each step?
The chain $J_{ISMq_{\sigma}} \sim J_{ESMq_{\sigma}} \sim J_{DSMq_{\sigma}} \sim J_{DAE}$ connects the concepts.
$J_{ISMq_{\sigma}} \sim J_{ESMq_{\sigma}}$ (Implicit $\to$ Explicit): Why: Integration by parts. This is Hyvärinen’s original proof allowing one to match the unknown data score by minimizing a term involving only the model’s score and its derivatives, assuming the density vanishes at infinity.
$J_{ESMq_{\sigma}} \sim J_{DSMq_{\sigma}}$ (Explicit $\to$ Denoising): Why: The explicit score of the Parzen density is known. When $x$ is perturbed to $\tilde{x}$ by Gaussian noise $\epsilon \sim \mathcal{N}(0, \sigma^2 I)$, the gradient of the log-density pointing back to the mean is exactly $\frac{1}{\sigma^2}(x - \tilde{x})$. Minimizing the error against the true score becomes minimizing the error against this restoration vector.
$J_{DSMq_{\sigma}} \sim J_{DAE}$ (Denoising $\to$ Autoencoder): Why: Algebraic substitution. If you define the model’s score $\psi(\tilde{x};\theta)$ to be proportional to the reconstruction error ($\propto x^r - \tilde{x}$), the score matching loss $J_{DSM}$ becomes proportional to the standard autoencoder squared loss $|x^r - x|^2$.
5. Energy-Based Models (EBMs) connection
What is an EBM?
An EBM defines a probability distribution via an energy function $E(x;\theta)$, where $p(x;\theta) \propto e^{-E(x;\theta)}$.
Why standard autoencoders aren’t probabilistic models:
A standard autoencoder is just a deterministic map $x \to x^r$. It lacks a normalization constant or a defined density function, meaning you cannot sample from it or ask “how probable is this input?” - it only provides a reconstruction error.
What does this enable?
By proving the equivalence, the DAE is formally defined as an EBM. This enables:
- Sampling: Using MCMC methods (like Hybrid Monte Carlo) to generate new data from the DAE.
- Ranking: Calculating the energy of inputs to determine which are more “likely” or “normal” (useful for anomaly detection).
6. The specific energy function form
The function is:
$$E(x; W, b, c) = - \frac{1}{\sigma^2} \left( \langle c, x \rangle - \frac{1}{2}||x||^2 + \sum_{j=1}^{d_h} \text{softplus}(\langle W_j, x \rangle + b_j) \right)$$
Why does it have that specific form?
It was derived via integration to ensure its derivative matches the DAE architecture. The authors worked backward from the DAE’s reconstruction function (sigmoid + linear) to find the scalar field that generates it.
Where does the quadratic term come from?
The score (derivative) needs to look like $\psi(x) \propto c + x + f(Wx + b)$.
- The term $+x$ (i.e., $\nabla_x (\frac{1}{2}|x|^2) = x$) in the derivative must come from a $-\frac{1}{2}|x|^2$ term in the energy potential.
How does differentiating it recover the DAE reconstruction?
- $\nabla_x \sum_j \text{softplus}(\langle W_j, x \rangle + b_j) = W^T \sigma(Wx + b)$ (The encoder part).
- $\nabla_x \langle c, x \rangle = c$ (The bias).
- $\nabla_x (-\frac{1}{2}|x|^2) = -x$ (The input subtraction).
- Result: $-\nabla_x E \propto c + W^T h - x = x^r - x$.
7. “Tied weights” justification
What does it mean for weights to be “tied”?
The decoder matrix is the transpose of the encoder matrix ($W^T$).
Why is this theoretically justified?
Because the reconstruction function is interpreted as the gradient of an energy function. A vector field can only be the gradient of a scalar field if its Jacobian is symmetric.
- In the DAE energy derivative, the encoder contributes $W^T \sigma(Wx + b)$. If the decoder used a separate matrix $U$, the resulting vector field would not be a valid gradient of any scalar energy function (unless $U = W^T$).
- Therefore, for a DAE to correspond to a valid probabilistic Energy-Based Model, the weights must be tied.
What was the alternative?
Before this proof, using tied weights was merely a heuristic or regularization choice. One could arbitrarily choose untied weights ($W$ and $U$), but this paper shows such a model loses its interpretation as a consistent score matching estimator.
Reproducibility Details
Since this is a theoretical paper, the “reproducibility” lies in the mathematical formulations derived.
Data
- Input Data ($D_n$): The theory assumes a set of training examples $D_n = {x^{(1)}, …, x^{(n)}}$ drawn from an unknown true pdf $q(x)$.
- Parzen Density Estimate ($q_{\sigma}$): The theoretical targets are derived from a kernel-smoothed empirical distribution: $$q_{\sigma}(\tilde{x}) = \frac{1}{n} \sum_{t=1}^n q_{\sigma}(\tilde{x}|x^{(t)})$$ where the kernel is an isotropic Gaussian of variance $\sigma^2$.
Algorithms
1. Denoising Score Matching (DSM) Objective
The paper proposes this objective as a tractable alternative to standard score matching. It minimizes the distance between the model score and the gradient of the log-noise density:
$$J_{DSMq_{\sigma}}(\theta) = \mathbb{E}_{q_{\sigma}(x,\tilde{x})} \left[ \frac{1}{2} \left| \psi(\tilde{x};\theta) - \frac{\partial \log q_{\sigma}(\tilde{x}|x)}{\partial \tilde{x}} \right|^2 \right]$$
For Gaussian noise, the target score is simply $\frac{1}{\sigma^2}(x - \tilde{x})$.
2. Equivalence Chain
The central result connects four objectives:
$$J_{ISMq_{\sigma}} \sim J_{ESMq_{\sigma}} \sim J_{DSMq_{\sigma}} \sim J_{DAE}$$
This implies optimizing the DAE reconstruction error is minimizing a score matching objective.
Models
1. The Denoising Autoencoder (DAE)
- Corruption: Additive isotropic Gaussian noise $\tilde{x} = x + \epsilon, \epsilon \sim \mathcal{N}(0, \sigma^2 I)$.
- Encoder: $h = \text{sigmoid}(W\tilde{x} + b)$.
- Decoder: $x^r = W^T h + c$ (Tied weights $W$).
- Loss: Squared reconstruction error $\frac{1}{2\sigma^4} ||x^r - x||^2$.
2. The Corresponding Energy Function
To make the DAE equivalent to Score Matching, the underlying Energy-Based Model $p(x;\theta) \propto e^{-E(x;\theta)}$ must have the following energy function:
$$E(x; W, b, c) = - \frac{1}{\sigma^2} \left( \langle c, x \rangle - \frac{1}{2}||x||^2 + \sum_{j=1}^{d_h} \text{softplus}(\langle W_j, x \rangle + b_j) \right)$$
Note the scaling by $1/\sigma^2$ and the quadratic term $||x||^2$.
Evaluation
- Metric: Theoretical Equivalence ($\sim$).
- Condition: The equivalence holds provided $\sigma > 0$ and the density $q_\sigma$ is differentiable and vanishes at infinity (regularity conditions for Score Matching).
Citation
@article{vincentConnectionScoreMatching2011,
title = {A {{Connection Between Score Matching}} and {{Denoising Autoencoders}}},
author = {Vincent, Pascal},
year = 2011,
month = jul,
journal = {Neural Computation},
volume = {23},
number = {7},
pages = {1661--1674},
doi = {10.1162/NECO_a_00142}
}