Relevance to Machine Learning
This 1997 paper establishes the mathematical foundations of displacement convexity in optimal transport theory, which underpins several modern generative modeling techniques. The displacement interpolation framework introduced here is used in:
- Flow Matching: Uses optimal transport probability paths (straight-line interpolations with constant speed) to generate samples. See the Flow Matching note for details on how OT paths differ from diffusion paths.
- Wasserstein GANs: Leverage the Wasserstein distance (optimal transport metric) for training stability.
- Continuous Normalizing Flows: Use OT-inspired transport maps for probability density transformation.
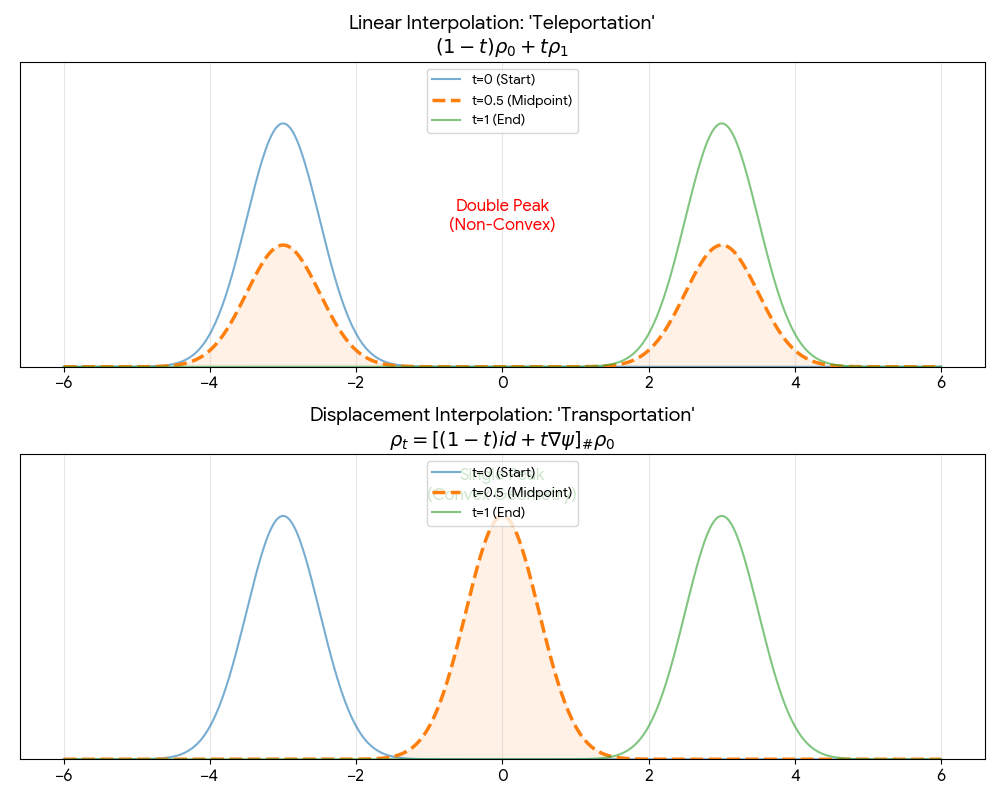
McCann’s convexity principle proves that energy functionals become convex along displacement paths even when non-convex under standard linear interpolation - a property exploited by modern generative models to ensure well-behaved training dynamics and unique solutions.
Paper Information
Citation: McCann, R. J. (1997). A Convexity Principle for Interacting Gases. Advances in Mathematics, 128(1), 153-179. https://doi.org/10.1006/aima.1997.1634
Publication: Advances in Mathematics 1997
What kind of paper is this?
This is a Theory paper ($\Psi_{\text{Theory}}$). It relies entirely on formal mathematical derivation to establish existence and uniqueness properties for energy functionals. It introduces a new mathematical structure (displacement interpolation) to analyze the geometry of probability measures.
What is the motivation?
The paper addresses the uniqueness of stationary configurations (ground states) for a gas model where particles interact via attractive forces while resisting compression.
- The Problem: The total energy functional $E(\rho)$ includes an interaction term $G(\rho)$ that is not convex under standard linear interpolation ($(1-t)\rho + t\rho’$), making it difficult to prove that a unique minimizer exists.
- The Gap: Standard convexity tools and rearrangement inequalities are insufficient for cases without specific symmetries (like spherical symmetry) or when convexity of the potential fails.
What is the novelty here?
The core novelty is the introduction of Displacement Interpolation.
- New Interpolant: The paper defines an interpolant $\rho_t$ by moving mass along the gradient of a convex potential $\psi$ (transport map).
- Displacement Convexity: It proves that the internal energy $U(\rho)$ and potential energy $G(\rho)$ - which are not convex under linear interpolation - become convex functions of $t$ along this displacement path.
- Generalization: This framework generalizes the classical Brunn-Minkowski inequality from sets to measures.
What experiments were performed?
No empirical or computational experiments were performed. The validation consists of rigorous mathematical proofs:
- Convexity Proofs: Deriving inequalities to show $E(\rho_t) \le (1-t)E(\rho) + tE(\rho’)$.
- Existence/Uniqueness: Using the new convexity principle to prove that the energy minimizer is unique up to translation.
What were the outcomes and conclusions drawn?
- Uniqueness of Ground State: For equations of state satisfying specific monotonicity conditions (e.g., polytropic gases), the energy minimizing state is unique up to translation.
- Brunn-Minkowski Extension: The internal energy convexity implies the Brunn-Minkowski inequality as a special case ($A(\rho) = -\rho^{(d-1)/d}$).
- Norm Concavity: The functional $||\rho_t||_q^{-p/d}$ is shown to be concave along the interpolation path for conjugate $p, q$.
Theoretical Framework
This section documents the key mathematical definitions and constructs that form the theoretical foundation of the paper.
Mathematical Setup
Probability Measures
The gas state is represented by absolutely continuous probability measures $\rho \in \mathcal{P}_{ac}(\mathbb{R}^d)$ with finite second moments.
Energy Functional
The gas model is defined by the total energy functional $E(\rho)$: $$E(\rho) := \underbrace{\int_{\mathbb{R}^d} A(\rho(x))dx}_{\text{Internal Energy } U(\rho)} + \underbrace{\frac{1}{2} \iint d\rho(x)V(x-y)d\rho(y)}_{\text{Potential Energy } G(\rho)}$$
Key Construction: Displacement Interpolation
The core theoretical tool is the construction of the interpolant $\rho_t$ between two probability measures $\rho$ and $\rho’$:
- Transport Map: By Brenier’s theorem, there exists a convex function $\psi$ such that $\nabla\psi_\rho = \rho’$ (push-forward).
- Interpolation: The interpolant at time $t \in [0,1]$ is defined as the push-forward of $\rho$ under the linear interpolation of the identity and the transport map: $$\rho_t := [(1-t)id + t\nabla\psi]_\rho$$
This is the “displacement interpolation” - mass moves along straight lines from initial to final positions.
Assumptions for Uniqueness
The uniqueness result requires three key assumptions:
- Interaction: $V(x)$ is strictly convex.
- Equation of State: The function $P(\rho)$ satisfies the condition that $P(\rho)/\rho^{(d-1)/d}$ is non-decreasing (equivalent to convexity of $U$ under dilation).
- Regularity: $\rho \in \mathcal{P}_{ac}(\mathbb{R}^d)$ (absolutely continuous probability measures).
Main Results
Theorem 2.2 (Displacement Convexity of Internal Energy): Under appropriate conditions on $A(\rho)$, the internal energy $U(\rho)$ is convex along displacement interpolation paths.
Theorem 3.1 (Existence and Uniqueness of Ground State): For polytropic gases and strictly convex interaction potentials $V$, the energy minimizer exists and is unique up to translation.
Lemma 3.2: Establishes formal bounds on the energy functional using the new convexity principle.
Connection to Brunn-Minkowski
The displacement convexity of internal energy generalizes the classical Brunn-Minkowski inequality. Setting $A(\rho) = -\rho^{(d-1)/d}$ recovers the geometric inequality as a special case, showing that the optimal transport framework unifies measure-theoretic and geometric convexity principles.
Citation
@article{mccannConvexityPrincipleInteracting1997,
title = {A {{Convexity Principle}} for {{Interacting Gases}}},
author = {McCann, Robert J.},
year = 1997,
month = jun,
journal = {Advances in Mathematics},
volume = {128},
number = {1},
pages = {153--179},
issn = {00018708},
doi = {10.1006/aima.1997.1634},
urldate = {2025-12-21}
}