Paper Information

Citation: Shannon, C. E. (1949). Communication in the Presence of Noise. Proceedings of the IRE, 37(1), 10-21. https://doi.org/10.1109/JRPROC.1949.232969

Publication: Proceedings of the IRE, 1949

What kind of paper is this?

This is a foundational Theory paper. It establishes the mathematical framework for modern information theory and defines the ultimate physical limits of communication for an entire system, from the information source to the final destination.

What is the motivation?

The central motivation was to develop a general theory of communication that could quantify information and determine the maximum rate at which it can be transmitted reliably over a noisy channel. Prior to this work, communication system design was largely empirical. Shannon sought to create a mathematical foundation to understand the trade-offs between key parameters like bandwidth, power, and noise, independent of any specific hardware or modulation scheme. To frame this, he conceptualized a general communication system as consisting of five essential elements: an information source, a transmitter, a channel, a receiver, and a destination.

What is the novelty here?

The novelty is a complete, end-to-end mathematical theory of communication built upon several groundbreaking concepts and theorems:

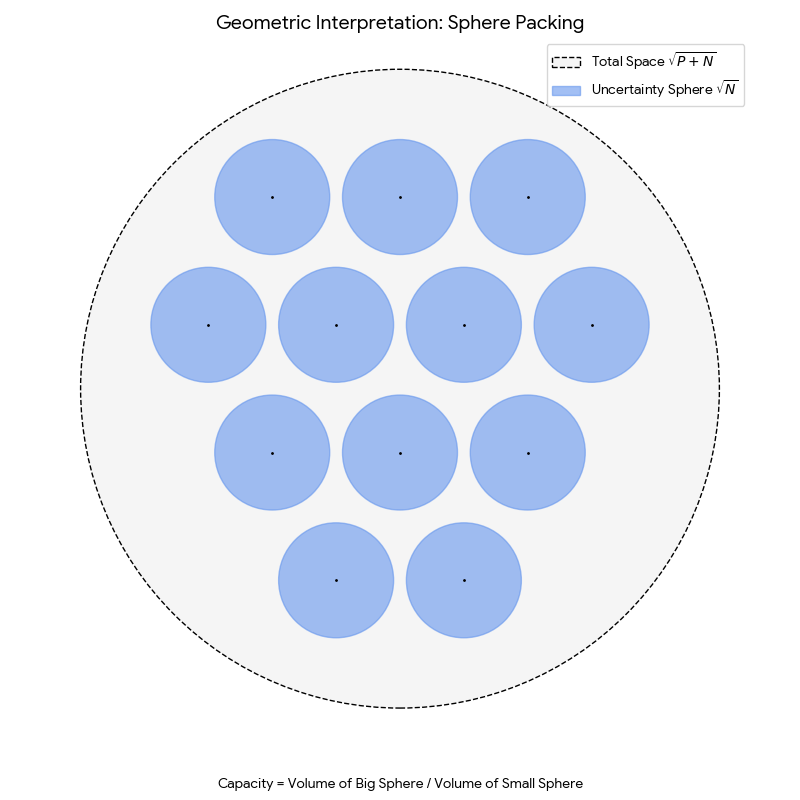
  1. Geometric Representation of Signals: Shannon introduced the idea of representing signals as points in a high-dimensional vector space. A signal of duration $T$ and bandwidth $W$ is uniquely specified by $2TW$ numbers (its samples), which are treated as coordinates in a $2TW$-dimensional space. This transformed problems in communication into problems of high-dimensional geometry. In this representation, signal energy corresponds to squared distance from the origin, and noise introduces a “sphere of uncertainty” around each transmitted point.
Sphere packing illustration showing the geometric interpretation of channel capacity. A large dashed circle represents the total signal space with radius proportional to the square root of P+N. Inside are multiple smaller blue circles (uncertainty spheres) with radius proportional to the square root of N, each centered on a distinct message point.
Sphere Packing and Channel Capacity: Each transmitted message corresponds to a point in high-dimensional signal space. Noise creates an ‘uncertainty sphere’ of radius $\sqrt{N}$ around each point. The channel capacity equals how many non-overlapping uncertainty spheres can be packed into the total signal sphere of radius $\sqrt{P+N}$.

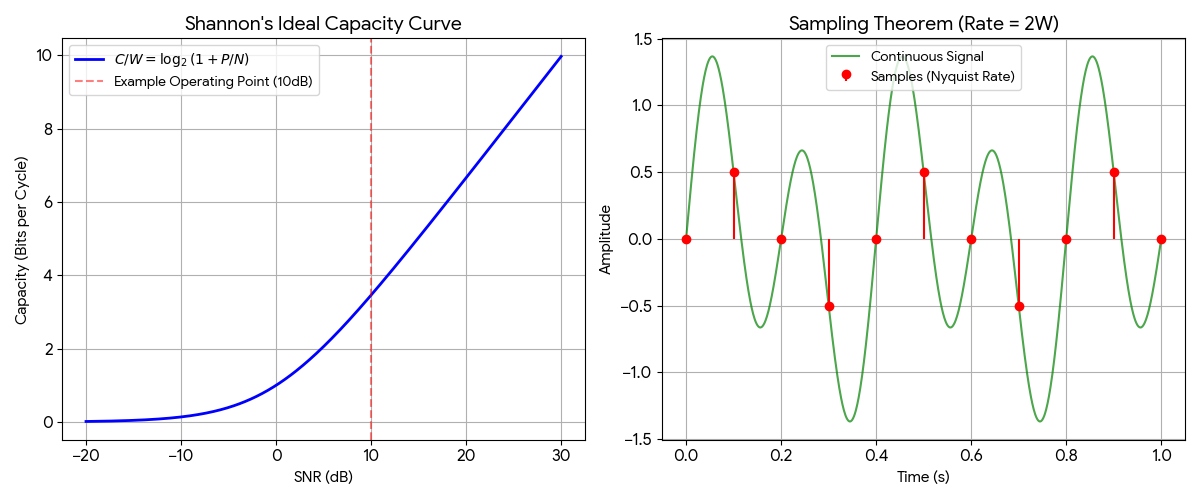
  1. Theorem 1 (The Sampling Theorem): The paper provides an explicit statement and proof that a signal containing no frequencies higher than $W$ is perfectly determined by its samples taken at a rate of $2W$ samples per second (i.e., spaced $1/2W$ seconds apart). Shannon explicitly credits Harry Nyquist for pointing out the fundamental importance of this time interval, formally naming it the “Nyquist interval” corresponding to the band $W$. This theorem is the theoretical bedrock of all modern digital signal processing.

  2. Theorem 2 (Channel Capacity for AWGN): This is the paper’s most celebrated result, the Shannon-Hartley theorem. It provides an exact formula for the capacity $C$ (the maximum rate of error-free communication) of a channel with bandwidth $W$, signal power $P$, and additive white Gaussian noise of power $N$: $$ C = W \log_2 \left(1 + \frac{P}{N}\right) $$ It proves that for any transmission rate below $C$, a coding scheme exists that can achieve an arbitrarily low error frequency.

Two plots illustrating Shannon's key theorems: (Left) The ideal capacity curve showing bits per cycle vs SNR in dB, with an example operating point at 10dB. (Right) The sampling theorem demonstrating how a continuous signal is perfectly captured by samples taken at the Nyquist rate of 2W.
Left: Shannon’s ideal capacity curve, showing how channel capacity (in bits per cycle) increases logarithmically with signal-to-noise ratio. Right: The sampling theorem in action, where a band-limited continuous signal is fully determined by discrete samples taken at twice its maximum frequency.
  1. Theorem 3 (Channel Capacity for Arbitrary Noise): Shannon generalized the capacity concept to channels with any type of noise. He showed that the capacity for a channel with arbitrary noise of power $N$ is bounded by the noise’s entropy power $N_1$ (a measure of its randomness). Critically, Shannon proved that white Gaussian noise is the worst possible type of noise for any given noise power, meaning it minimizes the channel capacity. This implies that systems designed to handle white Gaussian noise will perform even better against any other noise type of the same power.
The water-filling principle for optimal power allocation. Gray area shows noise power N(f) varying across frequencies, orange area shows signal power P(f) allocated to fill up to a constant level lambda, such that P(f) + N(f) equals a constant.
The Water-Filling Principle: A modern retrospective label for Shannon’s derivation. When noise power varies across frequencies, optimal capacity is achieved by allocating more signal power to ‘quieter’ frequency bands. Like filling a container with water, power is poured in until the total (signal + noise) reaches a constant level $\lambda$. Mathematically, Shannon derives that $P(f) + N(f)$ must be constant across the band for optimal capacity. Frequencies with noise above this threshold receive no power at all.

  1. Theorem 4 (Source Coding Theorem): This theorem addresses the information source itself. It proves that it’s possible to encode messages from a discrete source into binary digits such that the average number of bits per source symbol approaches the source’s entropy, $H$. This establishes entropy as the fundamental limit of data compression.

  2. Theorem 5 (Information Rate for Continuous Sources): For continuous (analog) signals, Shannon introduced a concept foundational to rate-distortion theory. He defined the rate $R$ at which a continuous source generates information relative to a specific fidelity criterion (i.e., a tolerable amount of error, $N_1$, in the reproduction). This provides the basis for all modern lossy compression algorithms.

What experiments were performed?

The paper is primarily theoretical, with “experiments” consisting of rigorous mathematical derivations and proofs. The channel capacity theorem, for instance, is proven using a geometric sphere-packing argument in the high-dimensional signal space.

However, Shannon does include a quantitative theoretical benchmark against existing 1949 technology. He plots his theoretical “Ideal Curve” against calculated limits of Pulse Code Modulation (PCM) and Pulse Position Modulation (PPM) systems in Figure 6. These were not physical laboratory experiments; the PCM points were calculated from formulas in another paper, and the PPM points were from unpublished calculations by B. McMillan. This comparison reveals that the entire series of plotted points for these contemporary systems operated approximately 8 dB below the ideal power limit over most of the practical range. Interestingly, PPM systems approached to within 3 dB of the ideal curve specifically at very small $P/N$ ratios, highlighting that different modulation schemes are optimal for different regimes (PCM for high SNR, PPM for power-limited scenarios).

What outcomes/conclusions?

The primary outcome was a complete, unified theory that quantifies both information itself (entropy) and the ability of a channel to transmit it (capacity).

  • Decoupling of Source and Channel: A key conclusion is that the problem of communication can be split into two distinct parts: encoding sequences of message symbols into sequences of binary digits (where the average digits per symbol approaches the entropy $H$), and then mapping these binary digits into a particular signal function of long duration to combat noise. A source can be transmitted reliably if and only if its rate $R$ (or entropy $H$) is less than the channel capacity $C$.

  • The Limit is on Rate, Not Reliability: Shannon’s most profound conclusion was that noise in a channel does not create an unavoidable minimum error rate; rather, it imposes a maximum rate of transmission. Below this rate, error-free communication is theoretically possible.

  • The Threshold Effect and Topological Necessity: To approach capacity, one must map a lower-dimensional message space into the high-dimensional signal space efficiently, like winding a “ball of yarn” to fill the available signal sphere. This complex mapping creates a sharp threshold effect: below a certain noise level, recovery is essentially perfect; above it, the system fails catastrophically because the “uncertainty spheres” around signal points begin to overlap. Shannon provides a profound topological explanation for why this threshold is unavoidable: it is impossible to continuously map a higher-dimensional space into a lower-dimensional one. To compress bandwidth (reduce dimensions), the mapping must be discontinuous; this necessary discontinuity creates the threshold where a small noise perturbation causes the signal to “jump” to a completely different interpretation. This explains the “cliff” behavior seen in digital communication systems, where performance is excellent until it suddenly isn’t.

  • The Exchange Relation: Shannon explicitly states that the key parameters $T$ (time), $W$ (bandwidth), $P$ (power), and $N$ (noise) can be “altered at will” as long as the channel capacity $C$ remains constant. This exchangeability is a fundamental insight for system architects, enabling trade-offs such as using more bandwidth to compensate for lower power.

  • Characteristics of an Ideal System: The theory implies that to approach the channel capacity limit, one must use very complex and long codes. An ideal system exhibits five key properties: (1) the transmission rate approaches $C$, (2) the error probability approaches zero, (3) the transmitted signal’s statistical properties approach those of white noise, (4) the threshold effect becomes very sharp (errors increase rapidly if noise exceeds the designed value), and (5) the required delay increases indefinitely. This final constraint is a crucial practical limitation: achieving near-capacity performance requires encoding over increasingly long message blocks, introducing latency that may be unacceptable for real-time applications.

Key Theoretical Insights

Random Coding: A Revolutionary Proof Technique

Shannon’s proof of the channel capacity theorem (Theorem 2) introduced a radical departure from traditional engineering approaches. Shannon employed a random coding argument: he proved that if you choose signal points at random from the sphere of radius $\sqrt{2TWP}$, the average error frequency vanishes for any transmission rate below capacity.

This non-constructive proof technique was revolutionary because it established that “good” codes exist almost everywhere in the signal space, even if we don’t know how to build them efficiently. The random coding argument became a fundamental tool in information theory, shifting the focus from building specific codes to proving existence and understanding fundamental limits.

The Topological Foundation of Thresholds

The sharp threshold effect in digital communication systems has a deep topological explanation. Shannon demonstrated that this phenomenon arises from a fundamental mathematical impossibility: continuously mapping a higher-dimensional space into a lower-dimensional one.

When we compress bandwidth (reducing the number of dimensions in signal space), the mapping from message space to signal space must necessarily be discontinuous. This required discontinuity creates vulnerable points where a small noise perturbation can cause the received signal to “jump” to an entirely different interpretation. The threshold is an inevitable consequence of dimensional reduction.

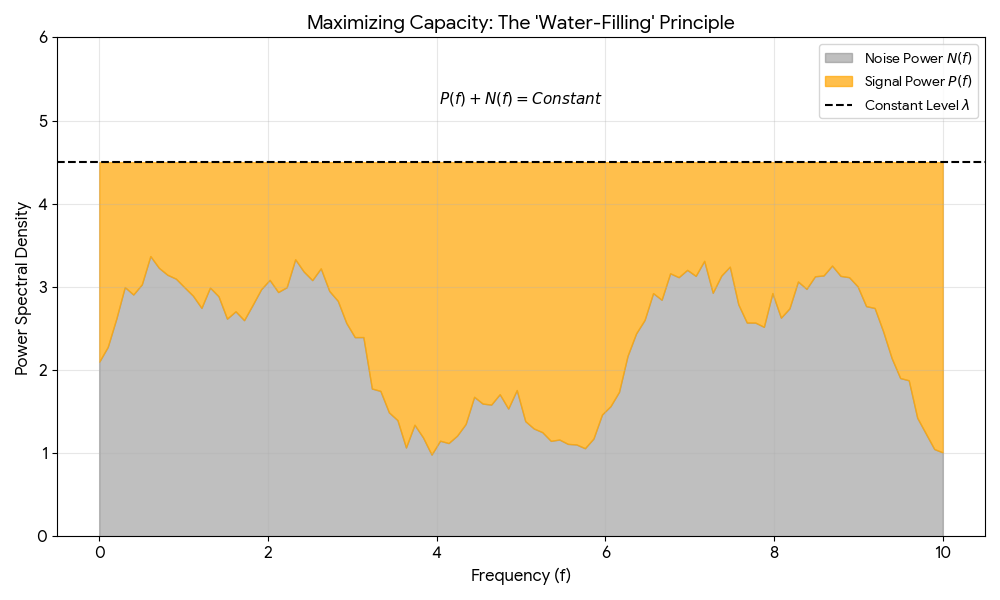
Arbitrary Gaussian Noise and the Water-Filling Principle

Shannon did not stop at analyzing white noise; he used the calculus of variations to determine how to maximize transmission when the noise spectrum $N(f)$ varies across frequencies. He proved that optimal capacity is achieved when the sum of the signal power $P(f)$ and noise power $N(f)$ is constant across the utilized frequency band.

This leads to what is now known as the “water-filling” principle (a modern retrospective label applied to Shannon’s exact mathematical condition): for frequencies where the noise power is low, the allocated signal power should be high, and vice versa. Frequencies where the noise exceeds the constant threshold receive no signal power at all. This mathematical derivation provides the foundation for modern techniques that dynamically allocate power across frequency bands based on channel conditions.

White Gaussian Noise as the Worst-Case Adversary

Theorem 3’s analysis of arbitrary noise types revealed a profound result: for any given noise power $N$, white Gaussian noise is the worst possible type of noise because it minimizes the channel capacity. The proof relies on the concept of entropy power, showing that among all noise distributions with the same variance, the Gaussian distribution has maximum entropy.

This worst-case property has important practical implications: if a communication system is designed to handle white Gaussian noise, it will perform even better against any other type of noise (such as impulse noise or colored noise) with the same power. Engineers can therefore design for the worst case with confidence that real-world performance will be no worse, and likely better.