Paper Information
Citation: Liu, Y., Chen, J., Jiao, R., Li, J., Huang, W., & Su, B. (2025). DenoiseVAE: Learning Molecule-Adaptive Noise Distributions for Denoising-based 3D Molecular Pre-training. International Conference on Learning Representations (ICLR).
Publication: ICLR 2025
Additional Resources:
What kind of paper is this?
This is a method paper with a supporting theoretical component. It introduces a new pre-training framework, DenoiseVAE, that challenges the standard practice of using fixed, hand-crafted noise distributions in denoising-based molecular representation learning.
What is the motivation?
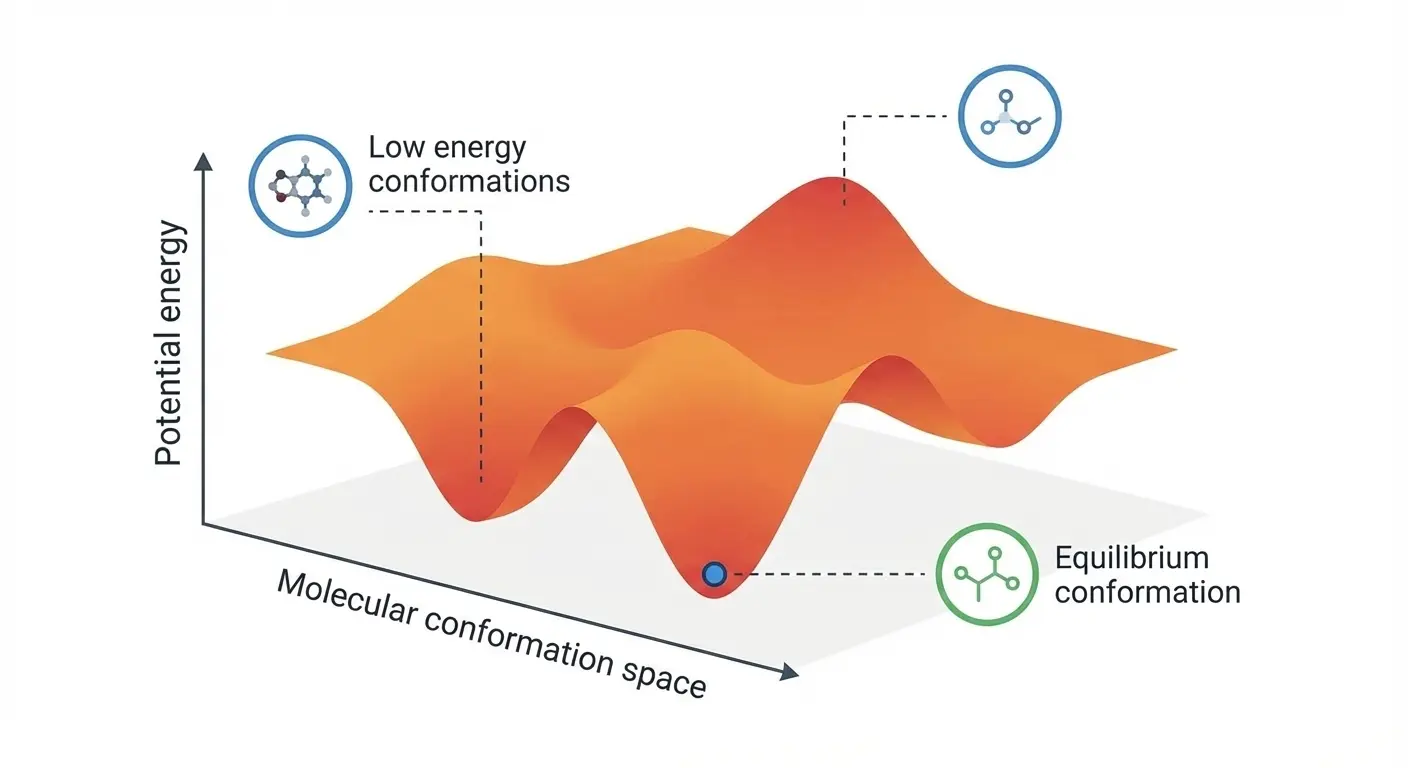
The motivation is to create a more physically principled denoising pre-training task for 3D molecules. The core idea of denoising is to learn molecular force fields by corrupting an equilibrium conformation with noise and then learning to recover it. However, existing methods use a single, hand-crafted noise strategy (e.g., Gaussian noise of a fixed scale) for all atoms across all molecules. This is physically unrealistic for two main reasons:
- Inter-molecular differences: Different molecules have unique Potential Energy Surfaces (PES), meaning the space of low-energy (i.e., physically plausible) conformations is highly molecule-specific.
- Intra-molecular differences (Anisotropy): Within a single molecule, different atoms have different degrees of freedom. For instance, an atom in a rigid functional group can move much less than one connected by a single, rotatable bond.
The authors argue that this “one-size-fits-all” noise approach leads to inaccurate force field learning because it samples many physically improbable conformations.
What is the novelty here?
The core novelty is a framework that learns to generate noise tailored to each specific molecule and atom. This is achieved through three key innovations:
- Learnable Noise Generator: The authors introduce a Noise Generator module (a 4-layer Equivariant Graph Neural Network) that takes a molecule’s equilibrium conformation $X$ as input and outputs a unique, atom-specific Gaussian noise distribution (i.e., a different variance $\sigma_i^2$ for each atom $i$). This directly addresses the issues of PES specificity and force field anisotropy.
- Variational Autoencoder (VAE) Framework: The Noise Generator (encoder) and a Denoising Module (a 7-layer EGNN decoder) are trained jointly within a VAE paradigm. The noisy conformation is sampled using the reparameterization trick: $\tilde{x}_i = x_i + \epsilon \sigma_i$.
- Principled Optimization Objective: The training loss $\mathcal{L}_{DenoiseVAE} = \mathcal{L}_{Denoise} + \lambda \mathcal{L}_{KL}$ balances two competing goals:
- A denoising reconstruction loss ($\mathcal{L}_{Denoise}$) encourages the Noise Generator to produce physically plausible perturbations from which the original conformation can be recovered. This implicitly constrains the noise to respect the molecule’s underlying force fields.
- A KL divergence regularization term ($\mathcal{L}_{KL}$) pushes the generated noise distributions towards a predefined prior. This prevents the trivial solution of generating zero noise and encourages the model to explore a diverse set of low-energy conformations.
The authors also provide a theoretical analysis showing that optimizing their objective is equivalent to maximizing the Evidence Lower Bound (ELBO) on the log-likelihood of observing physically realistic conformations.
What experiments were performed?
The model was pretrained on the PCQM4Mv2 dataset (approximately 3.4 million organic molecules) and then evaluated on a comprehensive suite of downstream tasks to test the quality of the learned representations:
- Molecular Property Prediction (QM9): The model was evaluated on 12 quantum chemical property prediction tasks for small molecules (134k molecules; 100k train, 18k val, 13k test split). DenoiseVAE achieved state-of-the-art or second-best performance on 11 of the 12 tasks, with particularly significant gains on $C_v$ (heat capacity), indicating better capture of vibrational modes.
- Force Prediction (MD17): The task was to predict atomic forces from molecular dynamics trajectories for 8 different small molecules (9,500 train, 500 val split). DenoiseVAE was the top performer on 5 of the 8 molecules, demonstrating its superior ability to capture dynamic properties.
- Ligand Binding Affinity (PDBBind v2019): On the PDBBind dataset, the model showed strong generalization, outperforming baselines like Uni-Mol particularly on the more challenging 30% sequence identity split.
- Ablation Studies: The authors analyzed the sensitivity to key hyperparameters, namely the prior’s standard deviation ($\sigma$) and the KL-divergence weight ($\lambda$), confirming that $\lambda=1$ and $\sigma=0.1$ are optimal. Removing the KL term leads to trivial solutions (zero noise).
- Case Studies: Visualizations of the learned noise variances for different molecules confirmed that the model learns chemically intuitive noise patterns. For example, it applies smaller perturbations to atoms in rigid bicyclic structures and larger ones to atoms in flexible functional groups.
Implementation details
For those looking to replicate this work, the authors used the AdamW optimizer with cosine learning rate decay (max LR of 0.0005) and a batch size of 128. The prior distribution has standard deviation $\sigma=0.1$, and the KL weight is $\lambda=1$.
The experiments were run on an Intel Xeon Gold 5318Y CPU @ 2.10GHz with a single RTX A3090 GPU, though the authors note that 6 GPUs with 144GB total memory are sufficient for full reproduction.
What were the outcomes and conclusions drawn?
- Primary Conclusion: Learning a molecule-adaptive and atom-specific noise distribution is a superior strategy for denoising-based pre-training compared to using fixed, hand-crafted heuristics. This more physically-grounded approach leads to representations that better capture molecular force fields.
- State-of-the-Art Performance: DenoiseVAE significantly outperforms previous methods across a diverse range of benchmarks, including property prediction, force prediction, and ligand binding affinity prediction. This demonstrates the broad utility and effectiveness of the learned representations.
- Effective Framework: The proposed VAE-based framework, which jointly trains a Noise Generator and a Denoising Module, is an effective and theoretically sound method for implementing this adaptive noise strategy. The interplay between the reconstruction loss and the KL-divergence regularization is key to its success.
- Future Direction: The work suggests that integrating more accurate physical principles and priors into the pre-training process is a promising direction for advancing 3D molecular representation learning.
Reproducibility Details
Data
- Pre-training Dataset: PCQM4Mv2 (approximately 3.4 million organic molecules)
- Property Prediction: QM9 dataset (134k molecules; 100k train, 18k val, 13k test split) for 12 quantum chemical properties
- Force Prediction: MD17 dataset (9,500 train, 500 val split) for 8 different small molecules
- Ligand Binding: PDBBind v2019 dataset
Algorithms
- Noise Generator: 4-layer Equivariant Graph Neural Network (EGNN) that outputs atom-specific Gaussian noise distributions
- Denoising Module: 7-layer EGNN decoder
- Training Objective: $\mathcal{L}{DenoiseVAE} = \mathcal{L}{Denoise} + \lambda \mathcal{L}_{KL}$ with $\lambda=1$
- Noise Sampling: Reparameterization trick with $\tilde{x}_i = x_i + \epsilon \sigma_i$
- Prior Distribution: Standard deviation $\sigma=0.1$
Models
- Model Size: 1.44M parameters total
- Fine-tuning Protocol: Noise Generator discarded after pre-training; only the pre-trained Denoising Module (7-layer EGNN) is retained with a 2-layer MLP prediction head
- Optimizer: AdamW with cosine learning rate decay (max LR of 0.0005)
- Batch Size: 128
- System Training: Fine-tuned end-to-end for specific tasks; force prediction involves computing the gradient of the predicted energy
Evaluation
- Ablation Studies: Sensitivity analysis confirmed $\lambda=1$ and $\sigma=0.1$ as optimal hyperparameters; removing the KL term leads to trivial solutions (zero noise)
- Rotational Constraints: Explicit rotational modeling provided only modest improvement (ZPVE metric: 0.015 to 0.017), suggesting the data-driven approach captures rotational constraints implicitly
- Covariance Structure: Full covariance matrix yielded comparable results to diagonal variance but with significantly increased computational overhead
Hardware
- Training Time: Approximately 25 hours for pre-training on PCQM4Mv2 (3.4M molecules)
- GPU Configuration: 6 NVIDIA RTX 3090 GPUs (24GB memory each, 144GB total)
- CPU: Intel Xeon Gold 5318Y @ 2.10GHz
- Minimum Requirements: Single RTX A3090 GPU sufficient for evaluation