Paper Information

Citation: Lu, S., Ji, X., Zhang, B., Yao, L., Liu, S., Gao, Z., Zhang, L., & Ke, G. (2025). Beyond Atoms: Enhancing Molecular Pretrained Representations with 3D Space Modeling. Proceedings of the 42nd International Conference on Machine Learning (ICML). https://proceedings.mlr.press/v267/lu25e.html

Publication: ICML 2025

Additional Resources:

What kind of paper is this?

This is a Method Paper. It challenges the atom-centric paradigm of molecular representation learning by proposing a novel framework that models the continuous 3D space surrounding atoms. The core contribution is SpaceFormer, a Transformer-based architecture that discretizes molecular space into grids to capture physical phenomena (electron density, electromagnetic fields) often missed by traditional point-cloud models.

What is the motivation?

The Gap: Prior 3D molecular representation models, such as Uni-Mol, treat molecules as discrete sets of atoms - essentially point clouds in 3D space. However, from a quantum physics perspective, the “empty” space between atoms is far from empty. It’s permeated by electron density distributions and electromagnetic fields that determine molecular properties.

The Hypothesis: Explicitly modeling this continuous 3D space (not just discrete atom positions) will yield superior representations for downstream tasks, particularly for computational properties that depend on electronic structure, such as HOMO/LUMO energies and energy gaps.

What is the novelty here?

The key innovation is treating the molecular representation problem as 3D space modeling rather than atom modeling. Instead of representing a molecule as a graph or point cloud of atoms, SpaceFormer:

  1. Voxelizes the entire 3D space into a grid with cells of $0.49\text{\AA}$ (based on O-H bond length)
  2. Uses adaptive multi-resolution grids to efficiently handle empty space - fine-grained near atoms, coarse-grained far away
  3. Applies Transformers to 3D spatial tokens with custom positional encodings:
    • 3D Directional PE: Extension of RoPE to capture relative directionality in continuous 3D space
    • 3D Distance PE: Random Fourier Features (RFF) to encode pairwise distances with linear complexity

This approach enables the model to capture field-like phenomena in the space between atoms, which traditional atom-centric models cannot represent.

What experiments were performed?

Pretraining Data: 19 million unlabeled molecules from the same dataset used by Uni-Mol.

Downstream Benchmarks: 15 tasks split into two categories:

  1. Computational Properties (Quantum Mechanics)

    • Subsets of GDB-17 (HOMO, LUMO, GAP energy prediction)
    • Polybenzenoid hydrocarbons (Dipole moment, ionization potential)
    • Metric: Mean Absolute Error (MAE)

  2. Experimental Properties (Pharma/Bio)

    • MoleculeNet tasks (BBBP, BACE for drug discovery)
    • Biogen ADME tasks (HLM, Solubility)
    • Metrics: AUC for classification, MAE for regression

Splitting Strategy: All datasets use 8:1:1 train/validation/test ratio with scaffold splitting to test out-of-distribution generalization.

Training Setup:

  • Objective: Masked Auto-Encoder (MAE) with 30% random masking. Model predicts whether a cell contains an atom, and if so, regresses both atom type and precise offset position.
  • Hardware: ~50 hours on 8 NVIDIA A100 GPUs
  • Optimizer: Adam ($\beta_1=0.9, \beta_2=0.99$)
  • Learning Rate: Peak 1e-4 with linear decay and 0.01 warmup ratio
  • Batch Size: 128
  • Total Updates: 1 million

Baseline Comparisons: Uni-Mol, Mol-AE, 3D Infomax, and other state-of-the-art molecular representation models.

What outcomes/conclusions?

State-of-the-Art Performance: SpaceFormer ranked 1st in 10 of 15 tasks and in the top 2 for 14 of 15 tasks.

Key Finding: The model significantly outperformed baselines (up to ~20% improvement) on computational properties like HOMO/LUMO energies, validating that modeling “empty” space captures electronic structure better than atom-only models.

Efficiency Validation: Ablation studies showed that Adaptive Grid Merging reduced the number of cells by an order of magnitude (roughly 10x compression) without performance loss.

Limitations Acknowledged:

  1. Not SE(3) Equivariant: Unlike geometric deep learning models (SchNet, Equiformer), SpaceFormer trades strict rotational/translational equivariance for computational efficiency. The model relies on data augmentation (random rotations) rather than architectural guarantees.

  2. Force Field Difficulty: Currently optimized for static property prediction, not molecular dynamics. Calculating forces ($F = -\nabla E$) requires first-order derivatives that are difficult to implement efficiently with FlashAttention. The model is unsuited for MD simulations.

  3. Experimental Task Performance: Less effective on noisy biological measurements (e.g., Blood-Brain Barrier Penetration). The authors attribute this to experimental variability - biological measurements are affected by temperature, biofilms, and inconsistent chemical representations.

Additional Validation: The model significantly outperformed Uni-Mol on the QM9 benchmark (a gold-standard quantum chemistry dataset) for HOMO/LUMO/GAP tasks, reinforcing the electronic structure prediction capabilities.

Future Directions: The work establishes a new paradigm for molecular pretraining, suggesting that space-centric rather than atom-centric modeling is a promising direction for the field.

Reproducibility Details

Model Architecture

The model treats a molecule as a 3D “image” via voxelization, processed by a Transformer.

Input Representation:

  • Discretization: 3D space divided into grid cells with length $0.49\text{\AA}$ (based on O-H bond length to ensure at most one atom per cell)
  • Tokenization: Tokens are pairs $(t_i, c_i)$ where $t_i$ is atom type (or NULL) and $c_i$ is the coordinate
  • Embeddings: Continuous embeddings with dimension 512. Inner-cell positions discretized with $0.01\text{\AA}$ precision

Transformer Specifications:

ComponentLayersAttention HeadsEmbedding DimFFN Dim
Encoder1685122048
Decoder (MAE)44256-

Attention Mechanism: FlashAttention for efficient handling of large sequence lengths.

Positional Encodings:

  1. 3D Directional PE: Extension of Rotary Positional Embedding (RoPE) to 3D continuous space, capturing relative directionality
  2. 3D Distance PE: Random Fourier Features (RFF) to approximate Gaussian kernel of pairwise distances with linear complexity

Visualizing RFF and RoPE

Four-panel visualization showing RFF distance encoding and RoPE directional encoding mechanisms
Visual intuition for SpaceFormer’s positional encodings: Top row shows RFF distance encoding (Gaussian-like attention decay and high-frequency feature fingerprints). Bottom row shows RoPE directional encoding (vector rotation fields and resulting attention patterns).

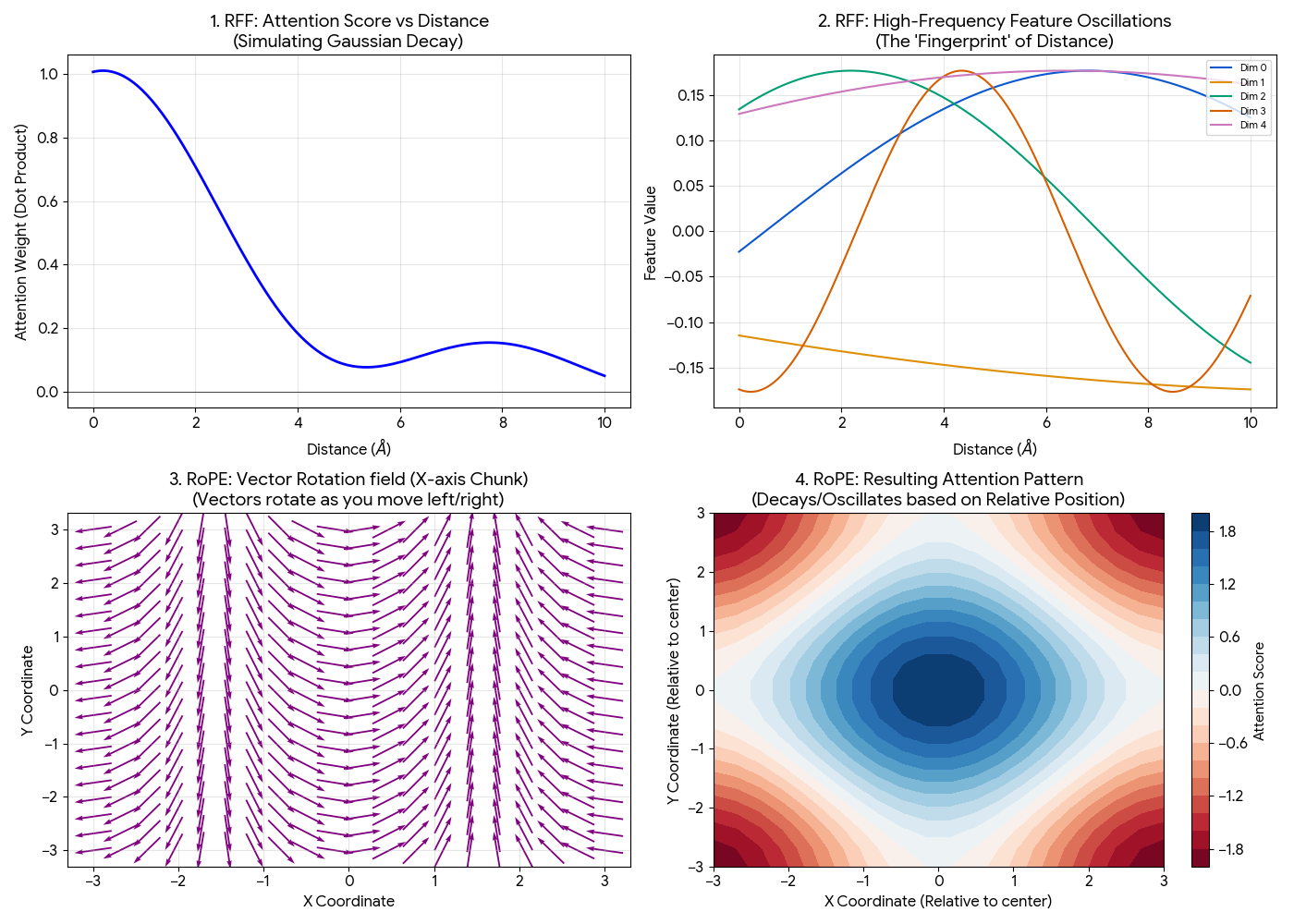
Top Row (Distance / RFF): Shows how the model learns “closeness.” Instead of a single number, distance is represented by a complex “fingerprint” of waves that creates a Gaussian-like force field.

  • Top Left (The Force Field): The attention score (dot product) naturally forms a Gaussian curve. It is high when atoms are close and decays to zero as they move apart. This mimics physical forces without the model needing to learn that math from scratch.
  • Top Right (The Fingerprint): Each dimension oscillates at a different frequency. A specific distance (e.g., $d=2$) has a unique combination of high and low values across these dimensions, creating a unique “fingerprint” for that exact distance.

Bottom Row (Direction / RoPE): Shows how the model learns “relative position.” It visualizes the vector rotation and how that creates a grid-like attention pattern.

  • Bottom Left (The Rotation): This visualizes the “X-axis chunk” of the vector. As you move from left ($x=-3$) to right ($x=3$), the arrows rotate. The model compares angles between atoms to determine relative positions.
  • Bottom Right (The Grid): The resulting attention pattern when combining X-rotations and Y-rotations. The red/blue regions show where the model pays attention relative to the center, forming a grid-like interference pattern that distinguishes relative positions (e.g., “top-right” vs “bottom-left”).

Adaptive Grid Merging

To make the 3D grid approach computationally tractable, two key strategies are employed:

  1. Grid Sampling: Randomly selecting 10-20% of empty cells during training
  2. Adaptive Grid Merging: Recursively merging $2 \times 2 \times 2$ blocks of empty cells into larger “coarse” cells, creating a multi-resolution view that is fine-grained near atoms and coarse-grained in empty space (merging set to Level 3)

Visualizing Adaptive Grid Merging:

2D simulation of adaptive grid merging for an H2O molecule showing multi-resolution cells
Adaptive grid merging demonstrated on H₂O. Red cells (Level 0) contain atoms and remain at full resolution. Progressively darker blue cells represent merged empty regions at higher levels, covering the same volume with fewer tokens.

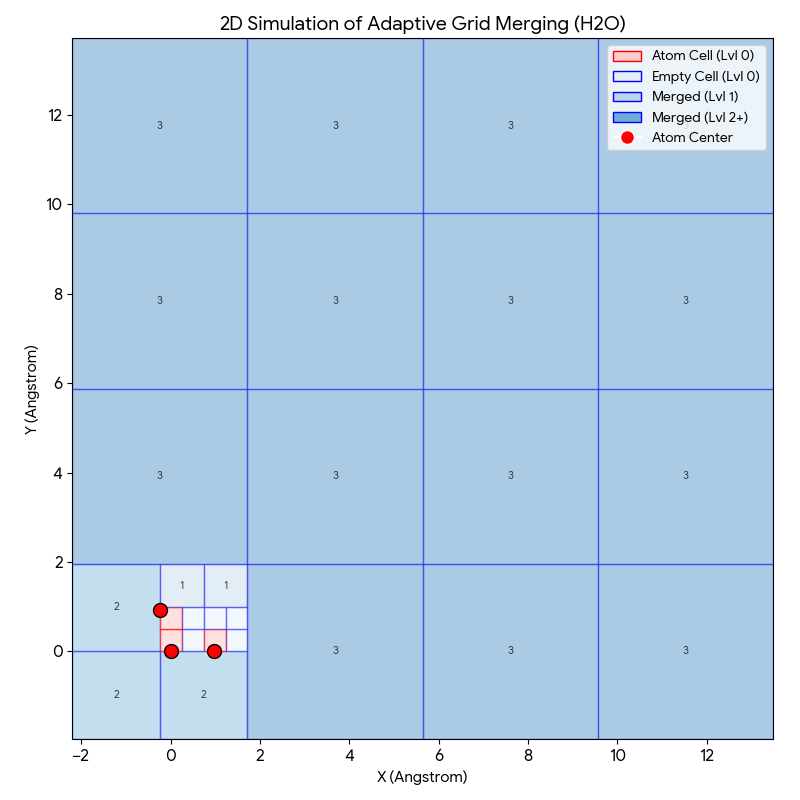
The adaptive grid process compresses empty space around molecules while maintaining high resolution near atoms:

  • Red Cells (Level 0): The smallest squares ($0.49$Å) containing atoms. These are kept at highest resolution because electron density changes rapidly here.
  • Light Blue Cells (Level 0/1): Small empty regions close to atoms.
  • Darker Blue Cells (Level 2/3): Large blocks of empty space further away.

If we used a naive uniform grid, we would have to process thousands of empty “Level 0” cells containing almost zero information. By merging them into larger blocks (the dark blue squares), the model covers the same volume with significantly fewer input tokens, reducing the number of tokens by roughly 10x compared to a dense grid.

Adaptive grid merging visualization for benzene molecule showing hexagonal ring with multi-resolution grid cells
Adaptive grid merging for benzene (C₆H₆). The model maintains maximum resolution (red Level 0 cells) only where atoms exist, while merging vast empty regions into large blocks (dark blue L3/L4 cells). This allows the model to focus computational power on chemically active zones.

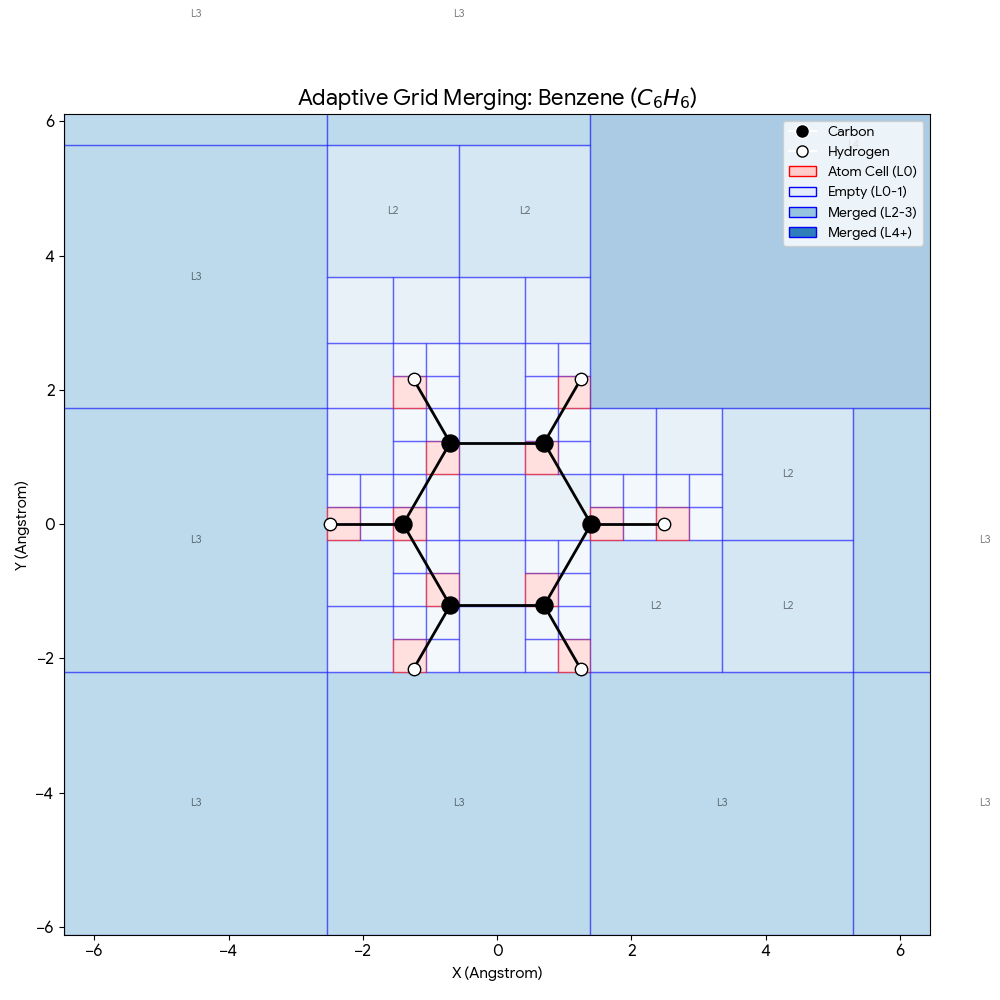
The benzene example above demonstrates how this scales to larger molecules. The characteristic hexagonal ring of 6 carbon atoms (black) and 6 hydrogen atoms (white) occupies a small fraction of the total grid. The dark blue corners (L3, L4) represent massive merged blocks of empty space, allowing the model to focus 90% of its computational power on the red “active” zones where chemistry actually happens.