Stillinger-Weber Potential for Silicon Simulation

Core Methodological Contribution

This is a Method paper.

Its primary contribution is the formulation of the Stillinger-Weber potential, a non-additive potential energy function designed to model tetrahedral semiconductors. The paper also uses molecular dynamics simulation to explore physical properties of silicon in both crystalline and liquid phases, but the methodological contribution (the potential architecture) is what enabled subsequent research on covalent materials.

The Failure of Pair Potentials in Silicon

The authors aimed to simulate the melting and liquid properties of tetrahedral semiconductors (Silicon and Germanium).

• The Problem: Standard pair potentials (like Lennard-Jones) favor close-packed structures (12 nearest neighbors) and cannot stabilize the open diamond structure (4 nearest neighbors) of Silicon.
• The Gap: Earlier classical potentials lacked the flexibility to describe the profound structural change where Silicon shrinks upon melting (coordination number increases from 4 to >6) while remaining conductive.
• The Goal: To construct a potential that spans the entire configuration space, describing both the rigid crystal and the diffusive liquid, without requiring quantum mechanical calculations.

The Three-Body Interaction Novelty

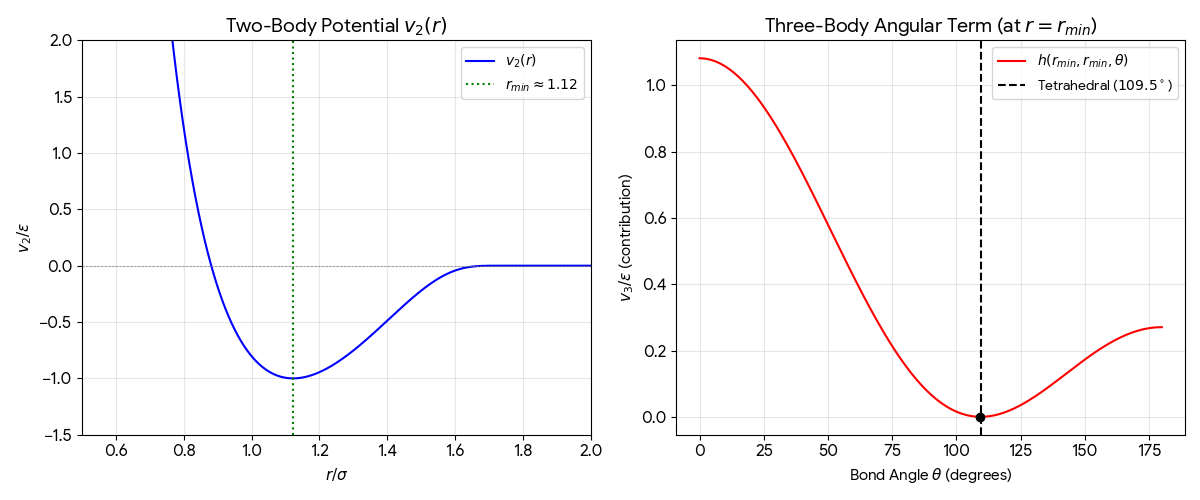
The core novelty is the introduction of a stabilizing three-body interaction term ($v_3$) to the potential energy function.

• 3-Body Term: Explicitly penalizes deviations from the ideal tetrahedral angle ($\cos \theta_t = -1/3$).
• Unified Model: This potential handles bond breaking and reforming, allowing for the simulation of melting and liquid diffusion. Previous “Keating” potentials model only small elastic deformations.
• Mapping Technique: The application of “steepest-descent mapping” to quench dynamical configurations into their underlying “inherent structures” (local minima), revealing the fundamental topology of the liquid energy landscape.

Molecular Dynamics Validation

The authors performed Molecular Dynamics (MD) simulations using the proposed potential.

• System: 216 Silicon atoms in a cubic cell with periodic boundary conditions.
• State Points: Fixed density $\rho = 2.53 \text{ g/cm}^3$ (matching experimental liquid density at melting).
• Process:
  1. Start with diamond crystal at low temperature.
  2. Systematically heat to induce spontaneous nucleation and melting.
  3. Equilibrate the liquid.
  4. Periodically map configurations to potential minima (inherent structures) using steepest descent.

Phase Topology and Inverse Lindemann Criterion

• Validation: The potential successfully stabilizes the diamond structure as the global minimum at zero pressure.
• Liquid Structure: The simulated liquid pair-correlation function $g(r)$ and structure factor $S(k)$ qualitatively match experimental diffraction data, including the characteristic shoulder on the structure factor peak.
• Inherent Structure: The liquid possesses a temperature-independent inherent structure (amorphous network) hidden beneath thermal vibrations.
• Melting/Freezing Criteria: The study proposes an “Inverse Lindemann Criterion”: while crystals melt when vibration amplitude exceeds ~0.19 lattice spacings, liquids freeze when atom displacements from their inherent minima drop below ~0.30 neighbor spacings.

Limitations and Energy Scale Problem

The authors acknowledge a quantitative energy scale discrepancy. To match the observed melting temperature of Si ($1410°$C), $\epsilon$ would need to be approximately 42 kcal/mol, considerably less than the 50 kcal/mol required to reproduce the correct cohesive energy of the crystal. The authors suggest this could be resolved either by further optimization of $v_2$ and $v_3$, or by adding position-independent single-particle terms $v_1 \approx -16$ kcal/mol arising from the electronic structure. Adding $v_1$ terms only affects the temperature scale and has no influence on local structure at a given reduced temperature.

The simulated liquid coordination number (8.07) is also higher than the experimentally reported value of approximately 6.4, though the authors note that the experimental definition of “nearest neighbors” was not precisely stated.

Bonding Statistics in Inherent Structures

Analysis of potential-energy minima (inherent structures) using a bond cutoff of $r/\sigma = 1.40$ reveals the coordination distribution in the liquid:

Five-coordinate atoms dominate the liquid’s inherent structure, with four- and six-coordinate atoms each accounting for about 20% of the population. The three-body interactions prevent any occurrence of coordination numbers near 12 that would indicate local close packing.

Reproducibility Details

Algorithms

• Integration: Equations of motion integrated using a fifth-order Gear algorithm.
• Time Step: $\Delta t = 5 \times 10^{-3} \tau$ (approx $3.83 \times 10^{-16}$ s), where $\tau = \sigma(m/\epsilon)^{1/2} = 7.6634 \times 10^{-14}$ s.
• Minimization: Steepest-descent mapping utilized Newton’s method to find limiting solutions ($\nabla \Phi = 0$).

Models

To reproduce this work, one must implement the potential $\Phi = \sum v_2 + \sum v_3$ with the exact functional forms and parameters provided.

Reduced Units

• $\sigma = 0.20951 \text{ nm}$
• $\epsilon = 50 \text{ kcal/mol} = 3.4723 \times 10^{-12} \text{ erg}$

Two-Body Term ($v_2$)

$$ v_2(r_{ij}) = \epsilon A (B r_{ij}^{-p} - r_{ij}^{-q}) \exp[(r_{ij} - a)^{-1}] \quad \text{for } r_{ij} < a $$

(Vanishes for $r \geq a$)

Three-Body Term ($v_3$)

$$ v_3(r_i, r_j, r_k) = \epsilon [h(r_{ij}, r_{ik}, \theta_{jik}) + h(r_{ji}, r_{jk}, \theta_{ijk}) + h(r_{ki}, r_{kj}, \theta_{ikj})] $$

where:

$$ h(r_{ij}, r_{ik}, \theta_{jik}) = \lambda \exp[\gamma(r_{ij}-a)^{-1} + \gamma(r_{ik}-a)^{-1}] (\cos\theta_{jik} + \frac{1}{3})^2 $$

(Vanishes if distances $\geq a$)

Parameters

Evaluation

The paper evaluates the model against experimental diffraction data.

Paper Information

Citation: Stillinger, F. H., & Weber, T. A. (1985). Computer simulation of local order in condensed phases of silicon. Physical Review B, 31(8), 5262-5271. https://doi.org/10.1103/PhysRevB.31.5262

Publication: Physical Review B, 1985

@article{stillingerComputerSimulationLocal1985,
  title = {Computer Simulation of Local Order in Condensed Phases of Silicon},
  author = {Stillinger, Frank H. and Weber, Thomas A.},
  year = 1985,
  month = apr,
  journal = {Physical Review B},
  volume = {31},
  number = {8},
  pages = {5262--5271},
  publisher = {American Physical Society},
  doi = {10.1103/PhysRevB.31.5262}
}