Paper Information

Citation: Daw, M. S., Foiles, S. M., & Baskes, M. I. (1993). The embedded-atom method: a review of theory and applications. Materials Science Reports, 9(7-8), 251-310. https://doi.org/10.1016/0920-2307(93)90001-U

Publication: Materials Science Reports 1993

Additional Resources:

What kind of paper is this?

This is a Systematization (Review) paper. It consolidates the theoretical development, semi-empirical parameterization, and broad applications of the Embedded-Atom Method (EAM) into a unified framework. The paper systematizes the field by connecting the EAM to related theories (Effective Medium Theory, Finnis-Sinclair, “glue” models) and organizing phenomenological results across diverse physical regimes (bulk, surfaces, interfaces).

The authors explicitly frame the work as a survey, stating “We review here the history, development, and application of the EAM” and “This review emphasizes the physical insight that motivated the EAM.” The paper follows a classic survey structure, organizing the literature not by a single hypothesis but by application domains.

What is the motivation?

The primary motivation is the failure of pair-potential models to accurately describe metallic bonding, particularly at defects and interfaces.

Physics Gap: Pair potentials assume bond strength is independent of environment, implying cohesive energy scales linearly with coordination ($Z$), whereas in reality it scales roughly as $\sqrt{Z}$.

Empirical Failures: Pair potentials incorrectly predict the “Cauchy relation” ($C_{12} = C_{44}$) and predict a vacancy formation energy equal to the cohesive energy, contradicting experimental data for fcc metals.

Practical Need: First-principles calculations (like DFT) were computationally too expensive for low-symmetry systems like grain boundaries and fracture tips, creating a need for an efficient, semi-empirical many-body potential.

What is the novelty here?

The paper’s core contribution is the synthesis of the EAM as a practical computational tool that captures “coordination-dependent bond strength” without the cost of ab initio methods.

Theoretical Unification: It demonstrates that the EAM ansatz can be derived from Density Functional Theory (DFT) by assuming the total electron density is a superposition of atomic densities.

Environmental Dependence: It explicitly formulates how the “effective” pair interaction stiffens and shortens as coordination decreases (e.g., at surfaces), a feature naturally arising from the non-linearity of the embedding function.

Broad Validation: It provides a centralized evaluation of the method across a vast array of metallic properties, establishing it as the standard for atomistic simulations of face-centered cubic (fcc) metals.

What experiments were performed?

The authors review computational experiments using Energy Minimization, Molecular Dynamics (MD), and Monte Carlo (MC) simulations across several domains:

Bulk Properties: Calculation of phonon spectra, liquid structure factors, thermal expansion coefficients, and melting points for fcc metals (Ni, Pd, Pt, Cu, Ag, Au).

Defects: Computation of vacancy formation/migration energies and self-interstitial geometries.

Surfaces: Analysis of surface energies, relaxations, reconstructions (e.g., Au(110) missing row), and surface phonons.

Alloys: Investigation of heat of solution, surface segregation profiles (e.g., Ni-Cu), and order-disorder transitions.

Mechanical Properties: Simulation of dislocation mobility, pinning by defects (He bubbles), and crack tip plasticity (ductile vs. brittle fracture modes).

What were the outcomes and conclusions drawn?

Many-Body Success: The EAM successfully reproduces the breakdown of the Cauchy relation and the correct ratio of vacancy formation energy to cohesive energy (~0.35) for fcc metals.

Surface Accuracy: It correctly predicts that surface bonds are shorter and stiffer than bulk bonds due to lower coordination. It accurately predicts surface reconstructions (e.g., Au(110) $(1 \times 2)$).

Alloy Behavior: The method naturally captures segregation phenomena, including oscillating concentration profiles in Ni-Cu, driven by the embedding energy rather than just bond-breaking.

Limitations: The method is less accurate for systems with strong directional bonding (covalent materials) or significant Fermi-surface effects, as it assumes spherically averaged electron densities.

Reproducibility Details

Data

Fitting Data: The semi-empirical functions are fitted to basic bulk properties: lattice constants, cohesive energy, elastic constants ($C_{11}$, $C_{12}$, $C_{44}$), and vacancy formation energy.

Universal Binding Curve: The cohesive energy as a function of lattice constant is constrained to follow the “universal binding curve” of Rose et al. to ensure accurate anharmonic behavior.

Alloy Data: For binary alloys, dilute heats of alloying are used for fitting cross-interactions.

Algorithms

Core Ansatz: The total energy is defined as:

$$E_{coh} = \sum_{i} G_i\left( \sum_{j \neq i} \rho_j^a(R_{ij}) \right) + \frac{1}{2} \sum_{i, j (j \neq i)} U_{ij}(R_{ij})$$

where $G$ is the embedding energy (function of local electron density $\rho$), and $U$ is a pair interaction.

Simulation Techniques:

  • Molecular Dynamics (MD): Used for liquids, phonons, and fracture simulations. Temperature control via velocity rescaling.
  • Monte Carlo (MC): Used for phase diagrams and segregation profiles (e.g., approximately $10^5$ iterations per atom).
  • Phonons: Calculated via the dynamical matrix derived from the force-constant tensor $K_{ij}$.

Models

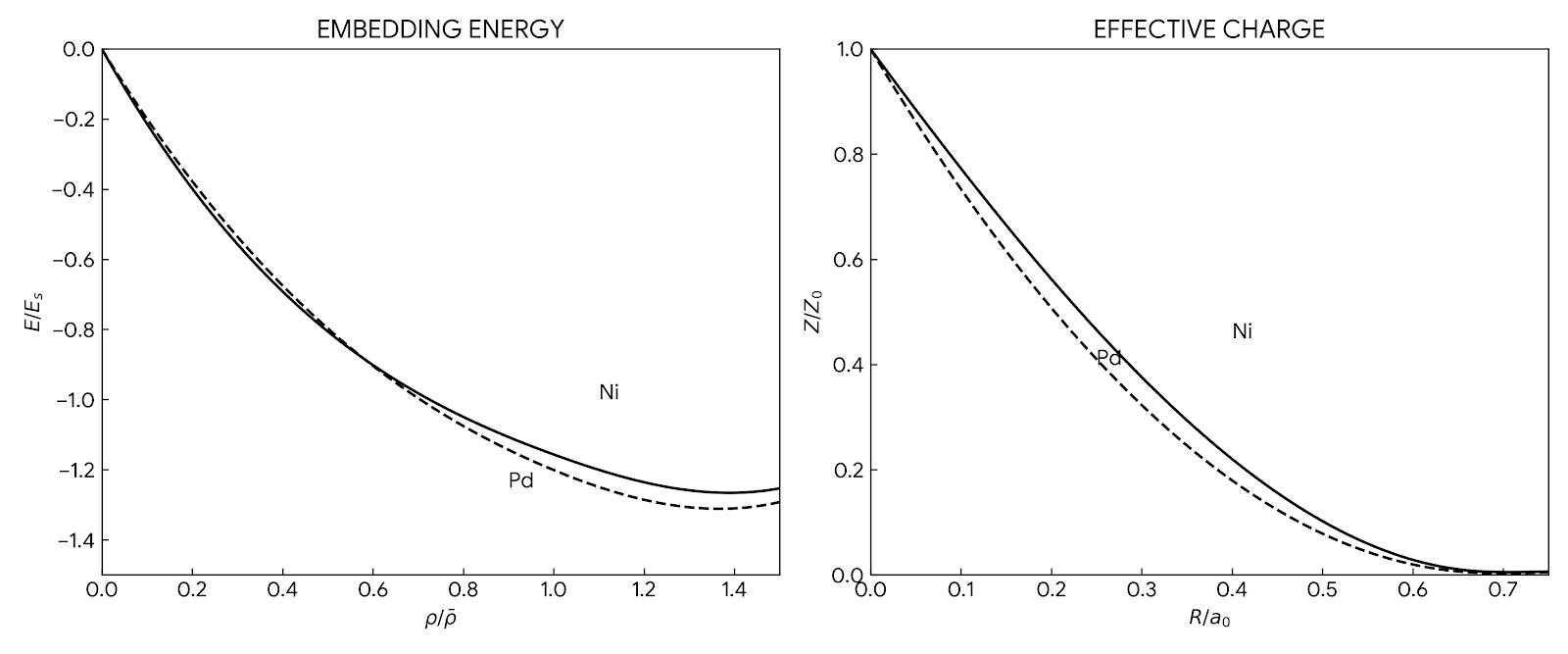
Parameterizations: The review lists several specific function sets developed by the authors, including:

  • Daw and Baskes: For Ni, Pd, H (spline-based)
  • Foiles: For Cu, Ag, Au, Ni, Pd, Pt (analytic functions)
  • Foiles: Specifically tailored for the Ni-Cu alloy system

Transferability: EAM functions are generally not transferable between different parameterization sets; mixing functions from different sets (e.g., Daw-Baskes Ni with Foiles Pd) is invalid.

Evaluation

Bulk Validation: Phonon dispersion curves for Cu show excellent agreement with experiment across the full Brillouin zone.

Thermal Properties: Linear thermal expansion coefficients match experiment well (e.g., Cu calculated: $16.4 \times 10^{-6}/K$ vs experimental: $16.7 \times 10^{-6}/K$).

Defect Energetics: Vacancy migration energies and divacancy binding energies (~0.1-0.2 eV) align with experimental data.

Surface Segregation: Correctly predicts segregation species for 18 distinct dilute alloy cases (e.g., Cu segregating in Ni).

Hardware

Compute Scale: At the time of publication (1993), Molecular Dynamics simulations of up to 35,000 atoms were possible.

Platforms: Calculations were performed on supercomputers like the CRAY-XMP, though smaller calculations were noted as feasible on high-performance workstations.

Citation

@article{dawEmbeddedatomMethodReview1993,
  title = {The embedded-atom method: a review of theory and applications},
  shorttitle = {The Embedded-Atom Method},
  author = {Daw, Murray S. and Foiles, Stephen M. and Baskes, Michael I.},
  year = 1993,
  month = mar,
  journal = {Materials Science Reports},
  volume = {9},
  number = {7},
  pages = {251--310},
  issn = {0920-2307},
  doi = {10.1016/0920-2307(93)90001-U}
}