Embedded-Atom Method: Impurities and Defects in Metals

Contribution: Adaptive Many-Body Potentials

This is a foundational method paper that introduces a new class of semi-empirical, many-body interatomic potential: the Embedded-Atom Method (EAM). It is designed for large-scale atomistic simulations of metallic systems, bridging the gap between computationally cheap (but physically limited) pair potentials and accurate (but expensive) quantum mechanical methods. The EAM achieves pair-potential speed while incorporating many-body physics inspired by density functional theory.

Motivation: The Geometric Limits of Pair Potentials

The authors sought to overcome the limitations of pair potentials (the dominant method of the time), which failed in three key areas:

• Elastic Anisotropy: Pair potentials enforce the Cauchy relation ($C_{12} = C_{44}$), which is violated by most transition metals.
• Volume Ambiguity: Pair potentials require a volume-dependent energy term, making them impossible to use accurately on surfaces or cracks where local volume is undefined.
• Chemical Incompatibility: Pair potentials cannot model chemically active impurities like Hydrogen.

First-principles quantum mechanical methods (e.g., band theory) are limited by basis-set size and periodicity requirements, making them impractical for the large systems (thousands of atoms) needed to study defects, surfaces, and mechanical properties.

The goal was to create a new model that bridges this gap in accuracy and computational cost.

Core Innovation: The Embedding Energy Function

The EAM postulates that the energy of an atom is determined by the local electron density of its neighbors. The total energy is:

$$E_{tot} = \sum_{i} F_i(\rho_{h,i}) + \frac{1}{2}\sum_{i \neq j} \phi_{ij}(R_{ij})$$

• $F_i(\rho_{h,i})$ (Embedding Energy): The energy required to embed atom $i$ into the background electron density $\rho$ provided by its neighbors. This term is non-linear and captures many-body effects.
• $\phi_{ij}$ (Pair Potential): A short-range electrostatic repulsion between cores.
• $\rho_{h,i}$ (Host Density): Approximated as a linear superposition of atomic densities: $\rho_{h,i} = \sum_{j \neq i} \rho^a_j(R_{ij})$.

The key innovations are:

1. The Embedding Energy: Each atom $i$ contributes an energy $F_i$ which is a non-linear function of the local electron density $\rho_{h,i}$ it is embedded in. This density is approximated as a simple linear superposition of the atomic electron densities of all its neighbors. This term captures the crucial many-body effects of metallic bonding.
2. A Redefined Pair Potential: A short-range, two-body potential $\phi_{ij}$ is retained, but it primarily models the electrostatic core-core repulsion.
3. Elimination of the “Volume” Problem: Because the embedding energy depends on the local electron density (a quantity that is always well-defined, even at a surface or a crack tip), the method circumvents the ambiguities of volume-dependent pair potentials.
4. Intrinsic Many-Body Nature: The non-linearity of the embedding function $F(\rho)$ naturally accounts for why chemically active impurities (like hydrogen) cannot be described by pair potentials and correctly breaks the Cauchy relation for elastic constants.

Experimental Design: Robust Parameter Validation

The authors validated EAM through a rigorous split between parameterization data and prediction tasks:

Fitting Data (Bulk Properties Only):

The model parameters were fitted exclusively to these experimental values for Ni and Pd:

• Lattice constant ($a_0$)
• Elastic constants ($C_{11}, C_{12}, C_{44}$)
• Sublimation energy ($E_s$)
• Vacancy-formation energy ($E^F_{1V}$)
• Hydrogen heat of solution (for fitting H parameters)

Validation Tests (No Further Fitting):

The model was then evaluated on its ability to predict these properties without any additional parameter adjustments:

• Surface Relaxations: Ni(110) surface contraction
• Surface Energy: Ni(100) surface energy
• Hydrogen Migration: H migration energy in Pd
• Fracture Mechanics: Hydrogen embrittlement in Ni slabs

Results: Extending Predictive Power to Surfaces and Defects

1. Many-Body Physics: The embedding function $F(\rho)$ successfully captures the volume-dependence of metallic cohesion, fixing the “Cauchy discrepancy” inherent in pair potentials.
2. Surface Properties: A single set of functions, fitted only to bulk data, correctly reproduces surface relaxations within 0.1 Å of experiment across three faces (100), (110), and (111) for Ni. The Ni(100) surface energy (1550 erg/cm²) compares well with the measured crystal-vapor average (1725 erg/cm²).
3. Hydrogen in Bulk: The method predicts H migration energy in Pd as 0.26 eV, matching experiment exactly. Hydride lattice expansions are also well reproduced: 4.5% for NiH (experiment: 5%) and 4% for PdH (experiment: 3.5% for PdH$_{0.6}$).
4. Hydrogen on Surfaces: Calculated adsorption sites on all three Ni and Pd faces agree with experimentally determined sites. Adsorption energies on Ni surfaces are systematically about 0.25 eV too low, while on Pd surfaces the error is much smaller (about 0.05 eV too high on average).
5. Fracture Mechanics: Static fracture calculations on Ni slabs demonstrate brittle fracture behavior and show that hydrogen lowers the fracture stress, providing a qualitative model of hydrogen embrittlement.

Limitations

The authors acknowledge several limitations:

• The functions $F$ and $\phi$ are not uniquely determined by the empirical fitting procedure. The short-range pair potential (restricted to first neighbors in fcc metals) may not be the best choice for all crystal structures.
• The choice of hydrogen embedding function (Puska et al. vs. Norskov’s corrected function) remains undecided and may affect hydrogen binding energies.
• The fracture calculations are static, and dynamical effects and plasticity play important roles in real fracture that are not captured.
• The method has only been demonstrated for fcc metals (Ni and Pd). Extension to bcc metals and other crystal structures requires further investigation.

Reproducibility Details

Algorithms

To replicate the method, three specific algorithmic definitions are needed:

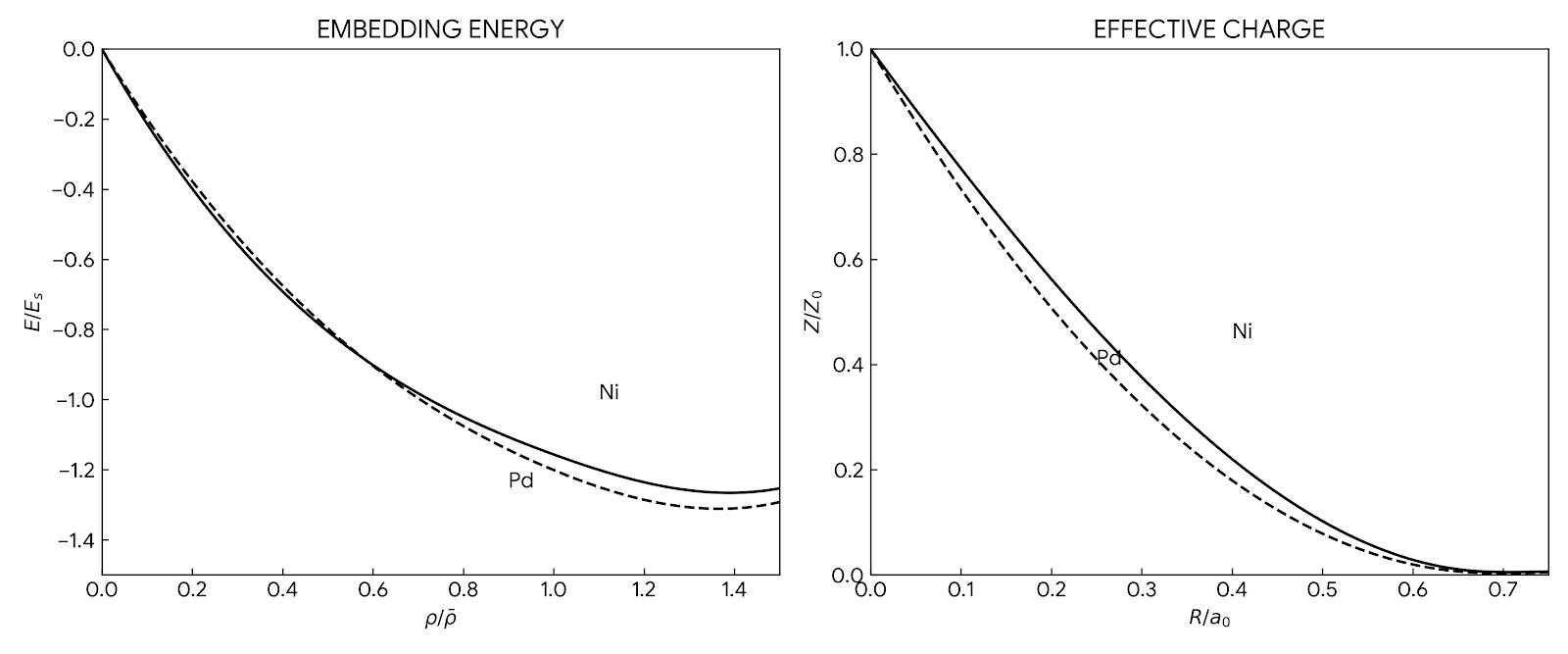
1. Atomic Density Construction: The electron density $\rho^a(r)$ is a weighted sum of Hartree-Fock $s$ and $d$ orbital densities (from Clementi & Roetti tables), controlled by a parameter $N_s$ (the number of s-like electrons): $$\rho^a(r) = N_s\rho_s^a(r) + (N-N_s)\rho_d^a(r)$$ For Ni, $N_s = 0.85$; for Pd, $N_s = 0.65$ (fitted to H solution heat).

2. Pair Potential Form: The short-range pair interaction derives from an effective charge function $Z(r)$ to handle core repulsion: $$\phi_{ij}(r) = \frac{Z_i(r)Z_j(r)}{r}$$ Splines for $Z(r)$ are provided in Table II.

3. Analytic Forces: Because embedding energy depends on neighbor density, the force calculation is many-body: $$\vec{f}_{k} = -\sum_{j(\neq k)} (F’_{k} \rho’_{j} + F’_{j} \rho’_{k} + \phi’_{jk}) \vec{r}_{jk}$$

Models

The functions $F(\rho)$ and $\phi(r)$ are modeled using cubic splines, with parameters fitted to reproduce bulk experimental constants. The embedding function $F(\rho)$ is constrained to have a single minimum and to be linear at high densities, matching the qualitative form of the first-principles calculations by Puska et al. Energy minimization uses the conjugate gradients technique. The paper explicitly lists spline knots, coefficients, and cutoffs in Tables II and IV, making the method fully reproducible.

Evaluation

Fitting Data (Used for Parameterization):

Bulk experimental properties for Ni and Pd only:

• Lattice constant ($a_0$)
• Elastic constants ($C_{11}, C_{12}, C_{44}$)
• Sublimation energy ($E_s$)
• Vacancy-formation energy ($E^F_{1V}$)
• Hydrogen heat of solution (for fitting H parameters)

Validation Results (Predictions Without Further Fitting):

Paper Information

Citation: Daw, M. S., & Baskes, M. I. (1984). Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Physical Review B, 29(12), 6443-6453. https://doi.org/10.1103/PhysRevB.29.6443

Publication: Physical Review B, 1984

@article{daw1984embedded,
  title={Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals},
  author={Daw, Murray S and Baskes, Mike I},
  journal={Physical Review B},
  volume={29},
  number={12},
  pages={6443--6453},
  year={1984},
  publisher={APS}
}

Additional Resources:

• EAM Review (1993)
• EAM User Guide (1994)
• NIST Interatomic Potentials Repository