Correlations in the Motion of Atoms in Liquid Argon

Contribution: Methodological Validation of MD

This is the archetypal Method paper (dominant classification with secondary Theory contribution). It establishes the architectural validity of Molecular Dynamics (MD) as a scientific tool. Rahman answers the question: “Can a digital computer solving classical difference equations faithfully represent a physical liquid?”

The paper utilizes specific rhetorical indicators of a methodological contribution:

• Algorithmic Explication: A dedicated Appendix details the predictor-corrector difference equations.
• Validation against Ground Truth: Extensive comparison of calculated diffusion constants and pair-correlation functions against experimental neutron and X-ray scattering data.
• Robustness Checks: Ablation studies on the numerical integration stability (one vs. two corrector cycles).

Motivation: Bridging Neutron Scattering and Many-Body Theory

In the early 1960s, neutron scattering data provided insights into the dynamic structure of liquids, but theorists lacked concrete models to explain the observed two-body dynamical correlations. Analytic theories were limited by the difficulty of the many-body problem.

Rahman sought to bypass these analytical bottlenecks by assuming that classical dynamics with a simple 2-body potential (Lennard-Jones) could sufficiently describe the motion of atoms in liquid argon. The goal was to generate “experimental” data via simulation to test theoretical models (like the Vineyard convolution approximation) and provide a microscopic understanding of diffusion.

Core Innovation: System Stability and the Cage Effect

This paper is widely considered the birth of modern molecular dynamics for continuous potentials. Its key novelties include:

1. System Size & Stability: Successfully simulating 864 particles interacting via a continuous Lennard-Jones potential with stable temperature over the full simulation duration (approximately $10^{-11}$ sec, as confirmed by Table I in the paper).
2. The “Cage Effect”: The discovery that the velocity autocorrelation function becomes negative after a short time: $$ \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle < 0 \quad \text{for } t > 0.33 \times 10^{-12} \text{ s} $$ This proved that atoms in a liquid “rattle” against the cage of their nearest neighbors.
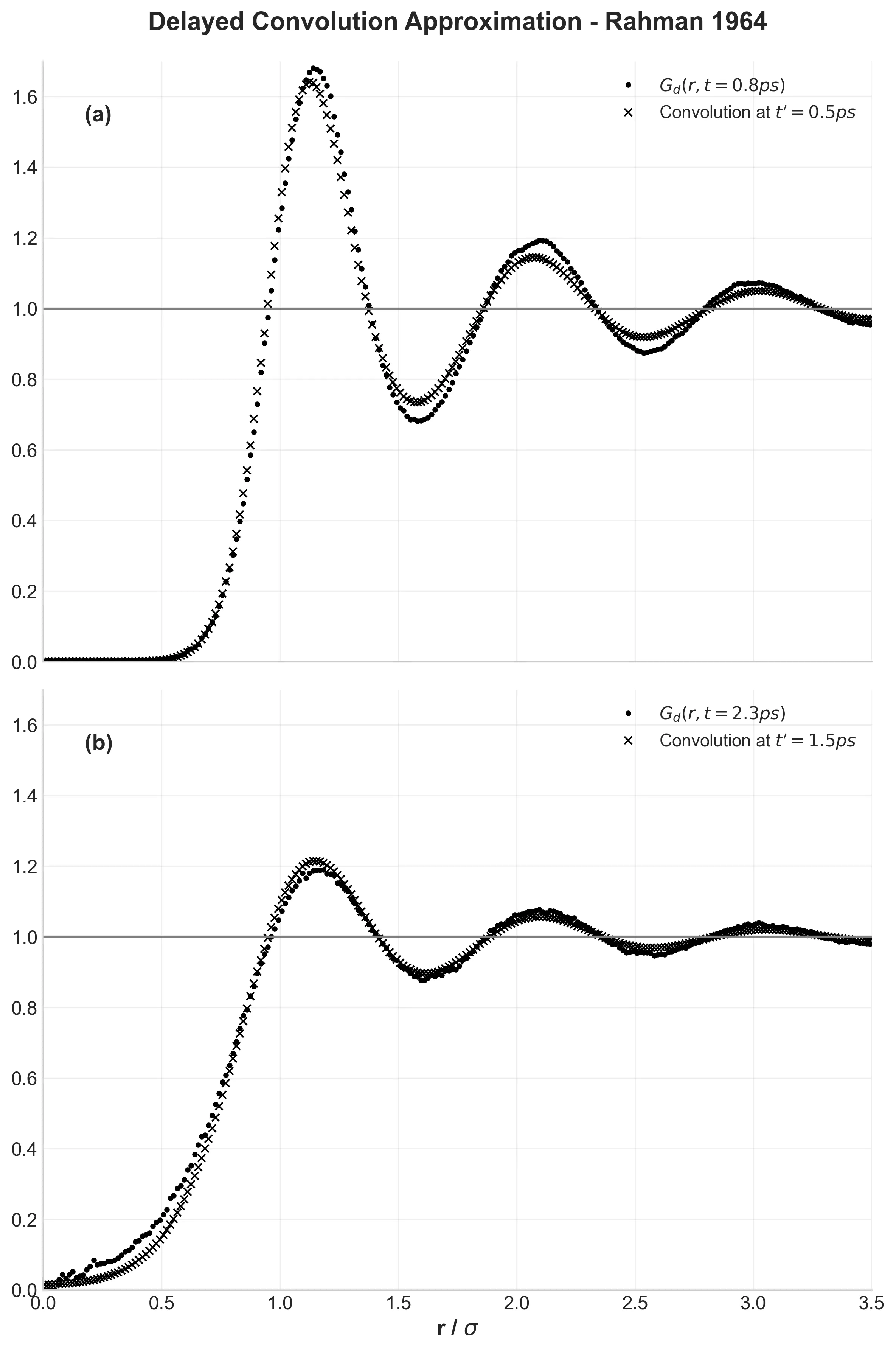
3. Delayed Convolution: Proposing an improvement to the Vineyard approximation for the distinct Van Hove function $G_d(r,t)$ by introducing a time-delayed convolution to account for the persistence of local structure. Instead of convolving $g(r)$ with $G_s(r,t)$ at the same time $t$, Rahman convolves at a delayed time $t’ < t$, using a one-parameter function with $\tau = 1.0 \times 10^{-12}$ sec. This makes $G_d(r,t)$ decay as $t^4$ at short times (instead of $t^2$ in the Vineyard approximation) and as $t$ at long times.

Methodology: Simulating 864 Argon Atoms

Rahman performed a “computer experiment” (simulation) of Liquid Argon:

• System: 864 particles in a cubic box of side $L=10.229\sigma$.
• Conditions: Temperature $94.4^\circ$K, Density $1.374 \text{ g cm}^{-3}$.
• Interaction: Lennard-Jones potential, truncated at $R=2.25\sigma$.
• Time Step: $\Delta t = 10^{-14}$ s (780 steps total, covering approximately $7.8 \times 10^{-12}$ s).
• Output Analysis:
  • Radial distribution function $g(r)$.
  • Mean square displacement $\langle r^2 \rangle$.
  • Velocity autocorrelation function $\langle v(0)\cdot v(t) \rangle$.
  • Van Hove space-time correlation functions $G_s(r,t)$ and $G_d(r,t)$.

Results: Validation and Non-Gaussian Diffusion Analysis

• Validation: The calculated pair-distribution function $g(r)$ agreed well with X-ray scattering data from Eisenstein and Gingrich (at $91.8^\circ$K). The self-diffusion constant $D = 2.43 \times 10^{-5} \text{ cm}^2 \text{ sec}^{-1}$ at $94.4^\circ$K matched the experimental value from Naghizadeh and Rice at $90^\circ$K and the same density ($1.374 \text{ g cm}^{-3}$).
• Dynamics: The velocity autocorrelation has a negative region, contradicting simple exponential decay models (Langevin). Its frequency spectrum $f(\omega)$ shows a broad maximum at $\omega \approx 0.25 (k_BT/\hbar)$, reminiscent of solid-like behavior.
• Non-Gaussian Behavior: The self-diffusion function $G_s(r,t)$ attains its maximum departure from a Gaussian shape at about $t \approx 3.0 \times 10^{-12}$ s (with $\langle r^4 \rangle$ departing from its Gaussian value by about 13%), returning to Gaussian form by $\sim 10^{-11}$ s. At that time, the rms displacement ($3.8$ Angstrom) is close to the first-neighbor distance ($3.7$ Angstrom). This indicates that Fickian diffusion is an asymptotic limit and does not apply at short times.
• Fourier Transform Validation: The Fourier transform of $g(r)$ has peaks at $\kappa\sigma = 6.8$, 12.5, 18.5, 24.8, closely matching the X-ray scattering peaks at $\kappa\sigma = 6.8$, 12.3, 18.4, 24.4.
• Temperature Dependence: A second simulation at $130^\circ$K and $1.16 \text{ g cm}^{-3}$ yielded $D = 5.67 \times 10^{-5} \text{ cm}^2 \text{ sec}^{-1}$, compared to the experimental value of $6.06 \times 10^{-5} \text{ cm}^2 \text{ sec}^{-1}$ from Naghizadeh and Rice at $120^\circ$K and $1.16 \text{ g cm}^{-3}$. The paper notes that both calculated values are lower than experiment by about 20%, and suggests that allowing for a softer repulsive part in the interaction potential might reduce this discrepancy.
• Vineyard Approximation: The standard Vineyard convolution approximation ($G_d \approx g * G_s$) produces a too-rapid decay of $G_d(r,t)$ with time. The delayed convolution, matching pairs of $(t’, t)$ in units of $10^{-12}$ sec as (0.2, 0.4), (0.5, 0.8), (1.0, 1.6), (1.5, 2.3), (2.0, 2.9), (2.5, 3.5), provides a substantially better fit.
• Conclusion: Classical N-body dynamics with a truncated pair potential is a sufficient model to reproduce both the structural and dynamical properties of simple liquids.

Reproducibility Details

Data

The simulation uses physical constants for Argon:

Algorithms

Rahman utilized a Predictor-Corrector scheme for solving the second-order differential equations of motion.

Step Size: $\Delta t = 10^{-14}$ sec.

The Algorithm:

1. Predict positions $\bar{\xi}$ at $t + \Delta t$ based on previous steps: $$\bar{\xi}_i^{(n+1)} = \xi_i^{(n-1)} + 2\Delta u \eta_i^{(n)}$$
2. Calculate Forces (Accelerations $\alpha$) using predicted positions.
3. Correct positions and velocities using the trapezoidal rule: $$ \begin{aligned} \eta_i^{(n+1)} &= \eta_i^{(n)} + \frac{1}{2}\Delta u (\alpha_i^{(n+1)} + \alpha_i^{(n)}) \\ \xi_i^{(n+1)} &= \xi_i^{(n)} + \frac{1}{2}\Delta u (\eta_i^{(n+1)} + \eta_i^{(n)}) \end{aligned} $$

Note: The paper compared one vs. two repetitions of the corrector step, finding that two passes improved precision slightly. The results presented in the paper were obtained using two passes.

Models

Interaction Potential: Lennard-Jones 12-6 $$V(r_{ij}) = 4\epsilon \left[ \left(\frac{\sigma}{r_{ij}}\right)^{12} - \left(\frac{\sigma}{r_{ij}}\right)^6 \right]$$

Boundary Conditions: Periodic Boundary Conditions (PBC) in 3 dimensions. When a particle moves out of the box ($x > L$), it re-enters at $x - L$.

Hardware

This is a historical benchmark for computational capability in 1964:

Modern Context: Rahman’s system (864 Argon atoms, LJ-potential) is highly reproducible today and serves as a classic pedagogical exercise. It can be simulated in standard MD frameworks (LAMMPS, OpenMM) in fractions of a second on consumer hardware.

Paper Information

Citation: Rahman, A. (1964). Correlations in the Motion of Atoms in Liquid Argon. Physical Review, 136(2A), A405-A411. https://doi.org/10.1103/PhysRev.136.A405

Publication: Physical Review 1964

@article{rahman1964correlations,
  title={Correlations in the motion of atoms in liquid argon},
  author={Rahman, A.},
  journal={Physical Review},
  volume={136},
  number={2A},
  pages={A405--A411},
  year={1964},
  publisher={APS},
  doi={10.1103/PhysRev.136.A405}
}

Additional Resources:

• Aneesur Rahman - Wikipedia