The Number of Isomeric Hydrocarbons of the Methane Series

A Theoretical Foundation for Mathematical Chemistry

This is a foundational theoretical paper in mathematical chemistry and chemical graph theory. It derives exact mathematical laws governing molecular topology. The paper also serves as a benchmark resource, establishing the first systematic isomer counts that corrected historical errors and whose recursive method remains the basis for modern molecular enumeration.

Historical Motivation and the Failure of Centric Trees

The primary motivation was the lack of a rigorous mathematical relationship between carbon content ($N$) and isomer count.

• Previous failures: Earlier attempts by Cayley (1875) (as cited by Henze and Blair, referring to the Berichte der deutschen chemischen Gesellschaft summary) and Schiff (1875) used “centric” and “bicentric” symmetry tree methods that broke down as carbon content increased, producing incorrect counts as early as $N = 12$. Subsequent efforts by Tiemann (1893), Delannoy (1894), Losanitsch (1897), Goldberg (1898), and Trautz (1924), as cited in the paper, each improved on specific aspects but none achieved general accuracy beyond moderate carbon content.
• The theoretical gap: All prior formulas depended on exhaustively identifying centers of symmetry, meaning they required additional correction terms for each increase in $N$ and could not reliably predict counts for larger molecules like $C_{40}$.

This work aimed to develop a theoretically sound, generalizable method that could be extended to any number of carbons.

Core Innovation: Recursive Enumeration of Graphs

The core novelty is the proof that the count of hydrocarbons is a recursive function of the count of alkyl radicals (alcohols) of size $N/2$ or smaller. The authors rely on a preliminary calculation of the total number of isomeric alcohols (the methanol series) to make this hydrocarbon enumeration possible. By defining $T_k$ as the exact number of possible isomeric alkyl radicals strictly containing $k$ carbon atoms, graph enumeration transforms into a mathematical recurrence.

To rigorously prevent double-counting when functionally identical branches connect to a central carbon, Henze and Blair applied combinations with substitution. Because the chemical branches are unordered topologically, connecting $x$ branches of identical structural size $k$ results in combinations with repetition:

$$ \binom{T_k + x - 1}{x} $$

For example, if a Group B central carbon is bonded to three identical sub-branches of length $k$, the combinatoric volume for that precise topological partition resolves to:

$$ \frac{T_k (T_k + 1)(T_k + 2)}{6} $$

Summing these constrained combinatorial partitions across all valid branch sizes (governed by the Even/Odd bisection rules) yields the exact isomer count for $N$ without overestimating due to symmetric permutations.

The Symmetry Constraints: The paper rigorously divides the problem space to prevent double-counting:

• Group A (Centrosymmetric): Hydrocarbons that can be bisected into two smaller alkyl radicals.
  • Even $N$: Split into two radicals of size $N/2$.
  • Odd $N$: Split into sizes $(N+1)/2$ and $(N-1)/2$.
• Group B (Asymmetric): Hydrocarbons whose graphic formula cannot be symmetrically bisected. They contain exactly one central carbon atom attached to 3 or 4 branches. To prevent double-counting, Henze and Blair established strict maximum branch sizes:
  • Even $N$: No branch can be larger than $(N/2 - 1)$ carbons.
  • Odd $N$: No branch can be larger than $(N-3)/2$ carbons.
  • The Combinatorial Partitioning: They further subdivided these 3-branch and 4-branch molecules into distinct mathematical cases based on whether the branches were structurally identical or unique, applying distinct combinatorial formulas to each scenario.

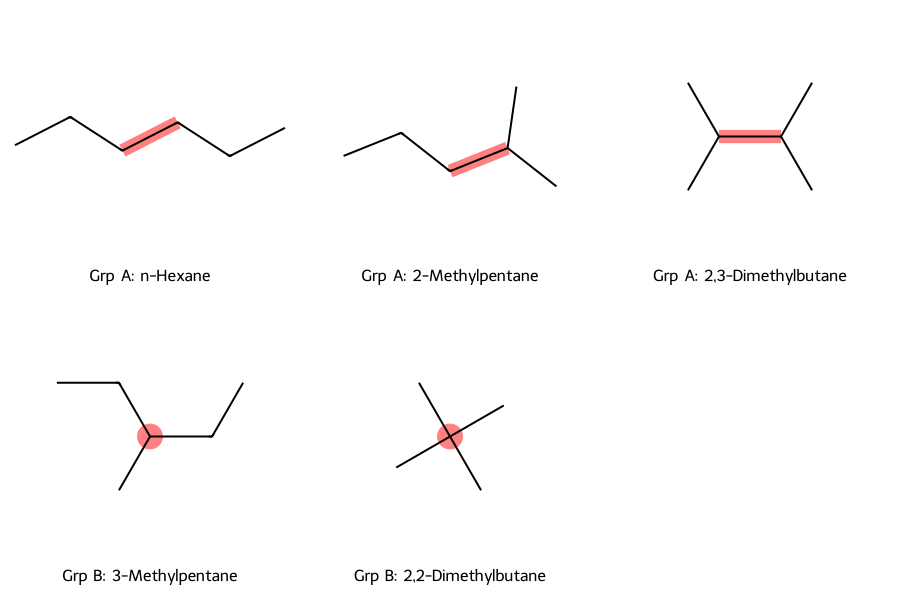
This classification is the key insight that enables the recursive formulas. By exhaustively partitioning hydrocarbons into these mutually exclusive groups, the authors could derive separate combinatorial expressions for each and sum them without double-counting.

For each structural class, combinatorial formulas are derived that depend on the number of isomeric alcohols ($T_k$) where $k < N$. This transforms the problem of counting large molecular graphs into a recurrence relation based on the counts of smaller, simpler sub-graphs.

Validation via Exhaustive Hand-Enumeration

The experiments were computational and enumerative:

1. Derivation of the recursion formulas: The main effort was the mathematical derivation of the set of equations for each structural class of hydrocarbon.
2. Calculation: They applied their formulas to calculate the number of isomers for alkanes up to $N=40$, reaching over $6.2 \times 10^{13}$ isomers. This was far beyond what was previously possible.
3. Validation by exhaustive enumeration: To prove the correctness of their theory, the authors manually drew and counted all possible structural formulas for the undecanes ($C_{11}$), dodecanes ($C_{12}$), tridecanes ($C_{13}$), and tetradecanes ($C_{14}$). This brute-force check confirmed their calculated numbers and corrected long-standing errors in the literature.
   • Key correction: The manual enumeration proved that the count for tetradecane ($C_{14}$) is 1,858, correcting the previously cited figure of 1,855 originally calculated by Losanitsch (1897) and later repeated by Trautz (1924), a value that had been, in the authors’ words, “accepted without further substantiation” into textbooks.

Benchmark Outcomes and Scaling Limits

• The Constitutional Limit: The paper establishes the mathematical ground truth for organic molecular graphs by strictly counting constitutional (structural) isomers. The derivation completely excludes 3D stereoisomerism (enantiomers and diastereomers). For modern geometric deep learning applications (e.g., generating 3D conformers), Henze and Blair’s scaling sequence serves as a lower bound, representing a severe underestimation of the true number of spatial configurations feasible within chemical space.
• Theoretical outcome: The paper proves that the problem’s inherent complexity requires a recursive approach.
• Benchmark resource: The authors published a table of isomer counts up to $C_{40}$ (Table II), correcting historical errors and establishing the first systematic enumeration across this range. Later computational verification revealed that the paper’s hand-calculated values are exact through at least $C_{14}$ (confirmed by exhaustive enumeration) but accumulate minor arithmetic errors beyond that range (e.g., at $C_{40}$). The recursive method itself is exact and remains the basis for the accepted values in OEIS A000602.

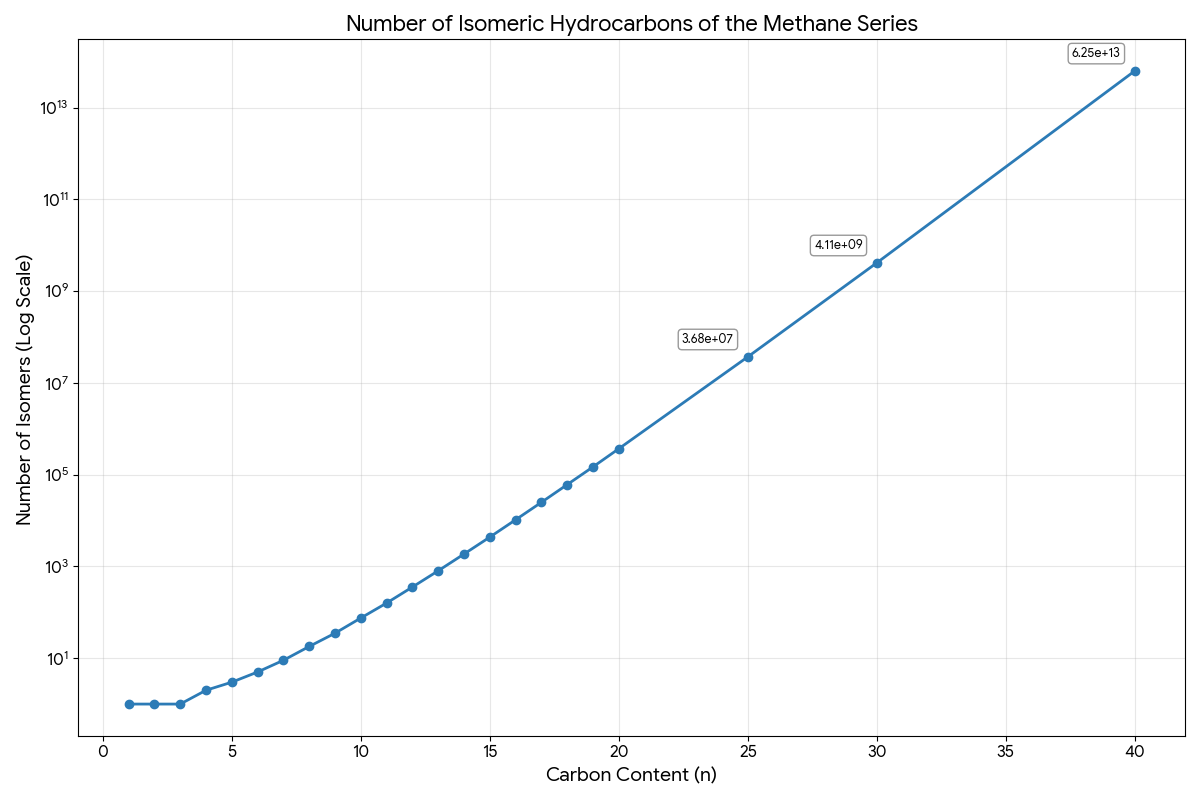
The plot above illustrates the staggering growth rate. Methane ($C_1$) through propane ($C_3$) each have exactly one isomer. Beyond this, the count accelerates rapidly: 75 isomers at $C_{10}$, nearly 37 million at $C_{25}$, and over 4 billion at $C_{30}$. By $C_{40}$, the count exceeds $6.2 \times 10^{13}$ (the paper’s hand-calculated Table II reports 62,491,178,805,831, while the modern OEIS-verified value is 62,481,801,147,341). This super-exponential scaling demonstrates why brute-force enumeration becomes impossible and why the recursive approach was essential.

• Foundational impact: This work established the mathematical framework that would later evolve into modern chemical graph theory and computational chemistry approaches for molecular enumeration. In the context of AI for molecular generation, this is an early form of expressivity analysis, defining the size of the chemical space that generative models must learn to cover.

Reproducibility Details

• Algorithms: The exact mathematical recursive formulas and combinatorial partitioning logic are fully provided in the text, allowing for programmatic implementation.

• Evaluation: The authors scientifically validated their recursive formulas through exhaustive manual hand-enumeration (brute-force drawing of structural formulas) up to $C_{14}$ to establish absolute correctness.

• Data: The paper’s Table II provides isomer counts up to $C_{40}$. These hand-calculated values are exact through at least $C_{14}$ (validated by exhaustive enumeration) but accumulate minor arithmetic errors beyond that range. The corrected integer sequence is maintained in the On-Line Encyclopedia of Integer Sequences (OEIS) as A000602.

• Code: The OEIS page provides Mathematica and Maple implementations. The following pure Python implementation uses the OEIS generating functions (which formalize Henze and Blair’s recursive method) to compute the corrected isomer counts up to any arbitrary $N$:

  def compute_alkane_isomers(max_n: int) -> list[int]:
      """
      Computes the number of alkane structural isomers C_nH_{2n+2}
      up to max_n using the generating functions from OEIS A000602.
      """
      if max_n == 0: return [1]
  
      # Helper: multiply two polynomials (cap at degree max_n)
      def poly_mul(a: list[int], b: list[int]) -> list[int]:
          res = [0] * (max_n + 1)
          for i, v_a in enumerate(a):
              for j, v_b in enumerate(b):
                  if i + j <= max_n: res[i + j] += v_a * v_b
                  else: break
          return res
  
      # Helper: evaluate P(x^k) by spacing out terms
      def poly_pow(a: list[int], k: int) -> list[int]:
          res = [0] * (max_n + 1)
          for i, v in enumerate(a):
              if i * k <= max_n: res[i * k] = v
              else: break
          return res
  
      # T represents the alkyl radicals (OEIS A000598), T[0] = 1
      T = [0] * (max_n + 1)
      T[0] = 1
  
      # Iteratively build coefficients of T
      # We only need to compute the (n-1)-th degree terms at step n
      for n in range(1, max_n + 1):
          # Extract previously calculated slices
          t_prev = T[:n]
  
          # T(x^2) and T(x^3) terms up to n-1
          t2_term = T[(n - 1) // 2] if (n - 1) % 2 == 0 else 0
          t3_term = T[(n - 1) // 3] if (n - 1) % 3 == 0 else 0
  
          # T(x)^2 and T(x)^3 terms up to n-1
          t_squared_n_1 = sum(t_prev[i] * t_prev[n - 1 - i] for i in range(n))
  
          t_cubed_n_1 = sum(
              T[i] * T[j] * T[n - 1 - i - j]
              for i in range(n)
              for j in range(n - i)
          )
  
          # T(x) * T(x^2) term up to n-1
          t_t2_n_1 = sum(
              T[i] * T[j]
              for i in range(n)
              for j in range((n - 1 - i) // 2 + 1)
              if i + 2*j == n - 1
          )
  
          T[n] = (t_cubed_n_1 + 3 * t_t2_n_1 + 2 * t3_term) // 6
  
      # Calculate Alkanes (OEIS A000602) from fully populated T
      T2 = poly_pow(T, 2)
      T3 = poly_pow(T, 3)
      T4 = poly_pow(T, 4)
      T_squared = poly_mul(T, T)
      T_cubed = poly_mul(T_squared, T)
      T_fourth = poly_mul(T_cubed, T)
  
      term2 = [(T_squared[i] - T2[i]) // 2 for i in range(max_n + 1)]
  
      term3_inner = [
          T_fourth[i]
          + 6 * poly_mul(T_squared, T2)[i]
          + 8 * poly_mul(T, T3)[i]
          + 3 * poly_mul(T2, T2)[i]
          + 6 * T4[i]
          for i in range(max_n + 1)
      ]
  
      alkanes = [1] + [0] * max_n
      for n in range(1, max_n + 1):
          alkanes[n] = T[n] - term2[n] + term3_inner[n - 1] // 24
  
      return alkanes
  
  # Calculate and verify
  isomers = compute_alkane_isomers(40)
  print(f"C_14 isomers: {isomers[14]}")   # Output: 1858
  print(f"C_40 isomers: {isomers[40]}")   # Output: 62481801147341
  

• Hardware: Derived analytically and enumerated manually by the authors in 1931 without computational hardware.

Paper Information

Citation: Henze, H. R., & Blair, C. M. (1931). The number of isomeric hydrocarbons of the methane series. Journal of the American Chemical Society, 53(8), 3077-3085. https://doi.org/10.1021/ja01359a034

Publication: Journal of the American Chemical Society (JACS) 1931

@article{henze1931number,
  title={The number of isomeric hydrocarbons of the methane series},
  author={Henze, Henry R and Blair, Charles M},
  journal={Journal of the American Chemical Society},
  volume={53},
  number={8},
  pages={3077--3085},
  year={1931},
  publisher={ACS Publications}
}