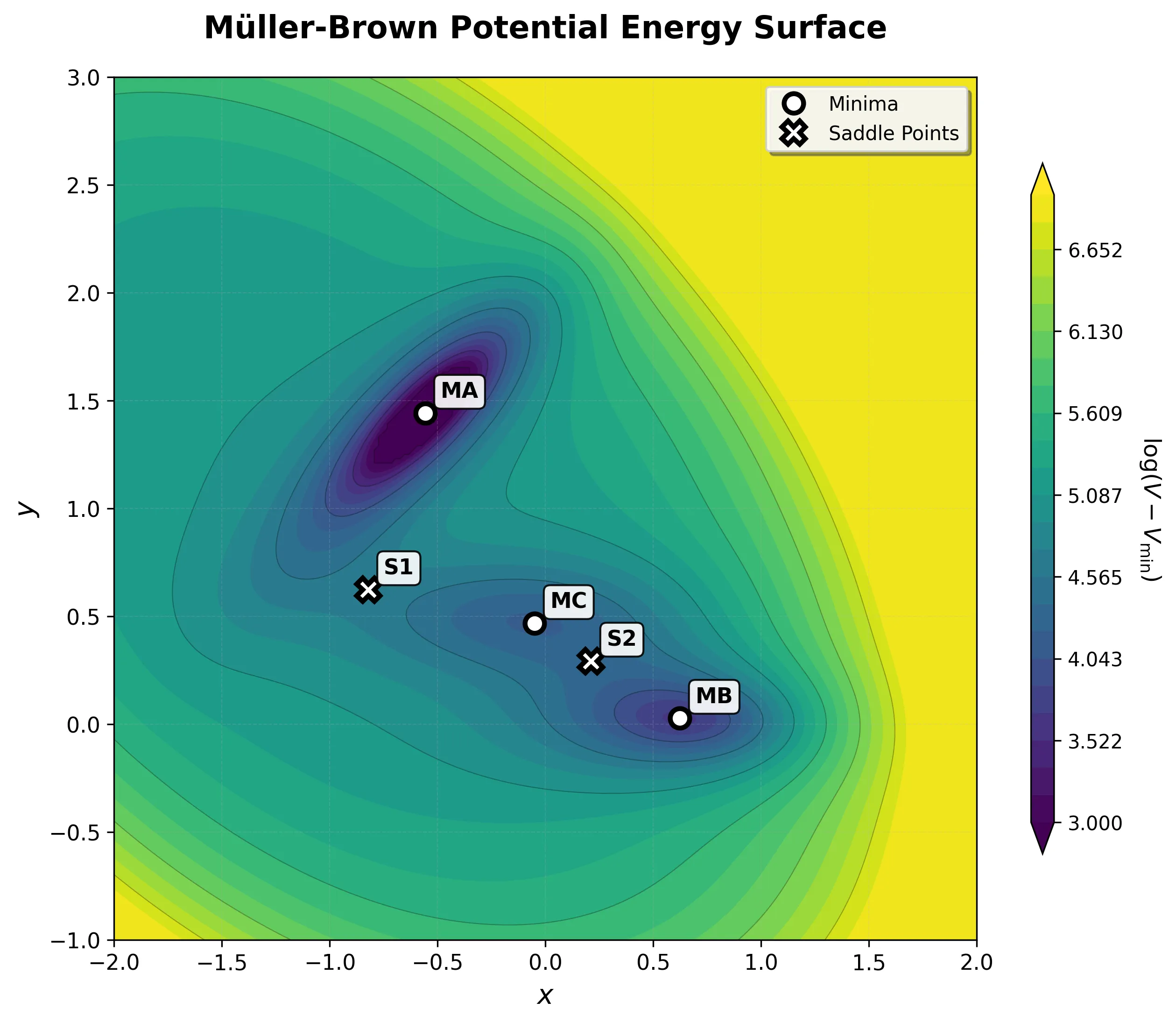
Müller-Brown Potential
The Müller-Brown potential: a classic two-dimensional analytical benchmark for testing optimization algorithms, reaction …...

The Müller-Brown potential: a classic two-dimensional analytical benchmark for testing optimization algorithms, reaction …...